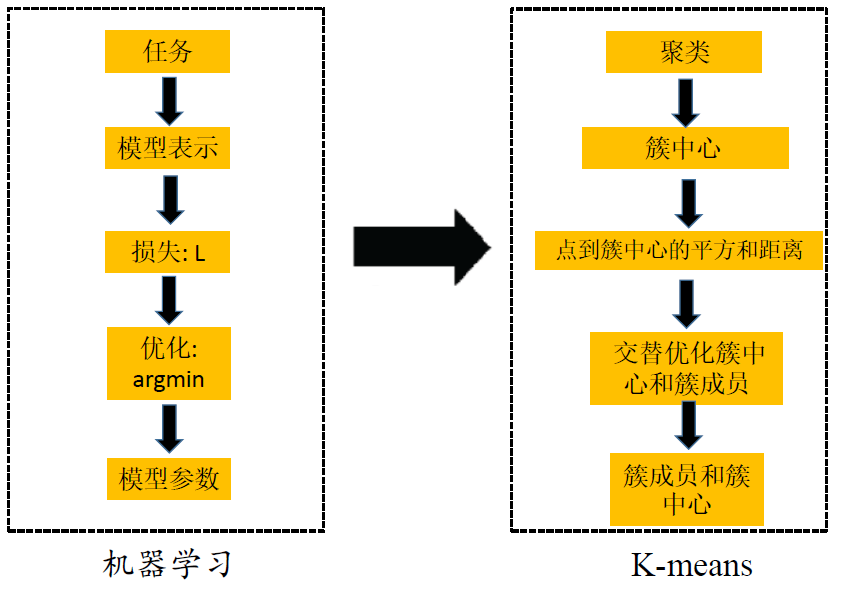
无监督学习的基本想法是对给定数据进行某种压缩,从而找到数据的潜在结构。(横向压缩、纵向压缩)
比如说对于一个训练数据 X m × n X_{m\times n} X m × n
X m × n = [ x 11 x 12 ⋯ x 1 n x 21 x 22 ⋯ x 2 n ⋮ ⋮ ⋱ ⋮ x m 1 x m 2 ⋯ x m n ] X_{m\times n}=
\begin{bmatrix}
x_{11}& x_{12}& \cdots & x_{1n} \\
x_{21}& x_{22}& \cdots & x_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
x_{m1}& x_{m2}& \cdots & x_{mn}
\end{bmatrix}
X m × n = ⎣ ⎢ ⎢ ⎢ ⎡ x 1 1 x 2 1 ⋮ x m 1 x 1 2 x 2 2 ⋮ x m 2 ⋯ ⋯ ⋱ ⋯ x 1 n x 2 n ⋮ x m n ⎦ ⎥ ⎥ ⎥ ⎤
训练数据由n个样本组成,每一个样本是一个M维的向量。每一行对应一个特征,每一列对应一个样本。
横向压缩(压缩特征):降维
纵向压缩(压缩样本):聚类
横向纵向:概率模型估计
K均值聚类:基于距离的聚类算法,采用距离作为相似性的评价指标,认为两个对象的距离越小,其相似度就越大。
首先,采用欧式距离平方,作为样本之间的距离 d ( x i , x j ) d({x_i},{x_j}) d ( x i , x j )
簇内任意一点到簇中心的距离:
d ( x , μ k ) 2 = ∥ x − μ k ∥ 2 = ( x − μ k ) T ( x − μ k ) {d}\left(\boldsymbol{x}, \boldsymbol{\mu}_{k}\right)^{2}=\left\|\boldsymbol{x}-\boldsymbol{\mu}_{k}\right\|^{2}=\left(\boldsymbol{x}-\boldsymbol{\mu}_{k}\right)^{\mathrm{T}}\left(\boldsymbol{x}-\boldsymbol{\mu}_{k}\right)
d ( x , μ k ) 2 = ∥ x − μ k ∥ 2 = ( x − μ k ) T ( x − μ k )
x = [ x 1 x 2 ⋯ x D ] T , μ k = [ μ k , 1 μ k , 2 ⋯ μ k , D ] T \boldsymbol{x}=\left[\begin{array}{llll}
x_{1} & x_{2} & \cdots & x_{D}
\end{array}\right]^{\mathrm{T}}, \quad \boldsymbol{\mu}_{k}=\left[\begin{array}{llll}
\mu_{k, 1} & \mu_{k, 2} & \cdots & \mu_{k, D}
\end{array}\right]^{\mathrm{T}}
x = [ x 1 x 2 ⋯ x D ] T , μ k = [ μ k , 1 μ k , 2 ⋯ μ k , D ] T
簇内距离平方和相当于残差平方和 (Sum of Squared Error, SSE),SSE可以度量样本数据的聚集程度。
S S E ( C K ) = ∑ x ∈ C k ∥ x − μ k ∥ 2 SSE(C_K)=\sum_{\boldsymbol{x} \in C_{k}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{k}\right\|^{2}
S S E ( C K ) = x ∈ C k ∑ ∥ x − μ k ∥ 2
然后,定义样本与其所属类的簇中心之间的距离总和为损失函数,即:
W ( C ) = ∑ k = 1 K ∑ x ∈ C k ∥ x − μ k ∥ 2 W(C)=\sum_{k=1}^{K} \sum_{\boldsymbol{x} \in C_{k}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{k}\right\|^{2}
W ( C ) = k = 1 ∑ K x ∈ C k ∑ ∥ x − μ k ∥ 2
W ( C ) W(C) W ( C )
因此,k均值聚类的优化问题为:
arg min C W ( C ) \underset{C}{\arg \min } W(C)
C arg min W ( C )
arg min C , μ ∑ k = 1 K ∑ x ∈ C k ∥ x − μ k ∥ 2 \underset{C, \boldsymbol{\mu}}{\arg \min } \sum_{k=1}^{K} \sum_{\boldsymbol{x} \in C_{k}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{k}\right\|^{2}
C , μ arg min k = 1 ∑ K x ∈ C k ∑ ∥ x − μ k ∥ 2
x \boldsymbol{x} x { x 1 , x 2 , … , x n } \left\{x_{1}, x_{2}, \ldots, x_{n}\right\} { x 1 , x 2 , … , x n }
C = { C 1 , C 2 , … , C K } C=\left\{C_{1}, C_{2}, \ldots, C_{K}\right\} C = { C 1 , C 2 , … , C K }
μ k \boldsymbol{\mu}_{k} μ k C K C_{K} C K
一共 K K K
∑ x ∈ C k ∥ x − μ k ∥ 2 \sum_{\boldsymbol{x} \in C_{k}}\left\|\boldsymbol{x}-\boldsymbol{\mu}_{k}\right\|^{2} ∑ x ∈ C k ∥ x − μ k ∥ 2
在这个目标函数中,有两个变量
{ 簇 中 心 : μ k 聚 类 结 果 : C \left\{\begin{matrix}簇中心:\boldsymbol{\mu}_{k}
\\聚类结果:C
\end{matrix}\right.
{ 簇 中 心 : μ k 聚 类 结 果 : C
换一种符号进行表达:
arg min { μ i , m j i } ∑ i = 1 K ∑ j = 1 n m j i ∥ x j − μ i ∥ 2 m j i = { 1 , 若 x j ∈ C i 0 , 若 x j ∉ C i \underset{\left\{\mu_{i}, m_{j i}\right\}}{\arg \min } \sum_{i=1}^{K} \sum_{j=1}^{n} m_{j i}\left\|x_{j}-\mu_{i}\right\|^{2} \\
\\
m_{j i}=\left\{\begin{array}{l}
1, \text { 若 } \mathrm{x}_{j} \in C_{i} \\
0, \text { 若 } \mathrm{x}_{j} \notin C_{i}
\end{array}\right.
{ μ i , m j i } arg min i = 1 ∑ K j = 1 ∑ n m j i ∥ x j − μ i ∥ 2 m j i = { 1 , 若 x j ∈ C i 0 , 若 x j ∈ / C i
这个 m j i m_{j i} m j i M ( n × K ) M(n \times K) M ( n × K )
M = [ 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 1 0 ⋯ 0 ] } ⏟ C 1 , C 2 , C 3 . . . , C K x 1 x 2 . . . x n M = \underbrace{\left . \begin{bmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
1 & 0 & \cdots & 0
\end{bmatrix} \right \}}_{\text C_1, C_2, C_3...,C_K}
\begin{matrix}
\\x_1
\\x_2
\\...
\\x_n
\\
\\
\end{matrix}
M = C 1 , C 2 , C 3 . . . , C K ⎣ ⎢ ⎢ ⎢ ⎡ 1 0 ⋮ 1 0 1 ⋮ 0 ⋯ ⋯ ⋱ ⋯ 0 0 ⋮ 0 ⎦ ⎥ ⎥ ⎥ ⎤ ⎭ ⎪ ⎪ ⎪ ⎬ ⎪ ⎪ ⎪ ⎫ x 1 x 2 . . . x n
每一行只有一个元素为1,其他都是0。因为每一个样本只能归为一个簇(硬分类)。
在这个目标函数中,有两个变量:
{ 簇 中 心 : μ k 聚 类 结 果 : m i j \left\{\begin{matrix}簇中心:\boldsymbol{\mu}_{k}
\\聚类结果:m_{ij}
\end{matrix}\right.
{ 簇 中 心 : μ k 聚 类 结 果 : m i j
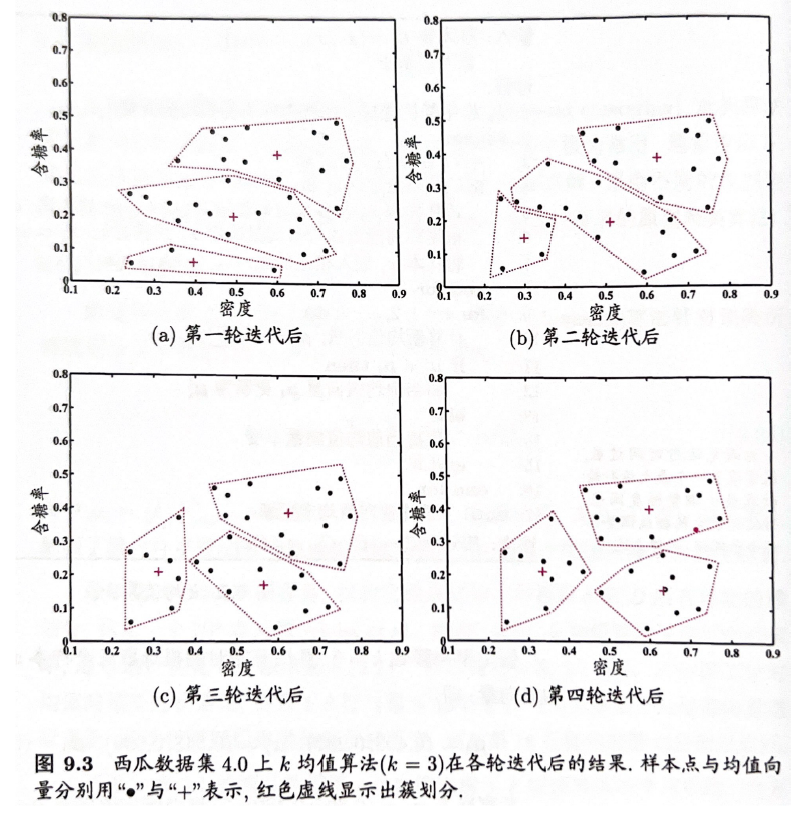
对于这样的有两组变量的优化问题,是一个NP难的问题。所以实际中,我们采用交替优化的方法进行求解。(固定一个参数,优化另一个,一直这样迭代)
分为两步:
更新簇成员:选择k个类的簇中心,将样本分类到离他最近的簇中心里。(得到聚类结果)(固定μ k \boldsymbol{\mu}_{k} μ k C C C
更新簇中心:计算每个类的样本均值作为新的簇中心。(得到μ k \boldsymbol{\mu}_{k} μ k C C C μ k \boldsymbol{\mu}_{k} μ k
f o r j = 1 , 2 , . . . , m : 计 算 样 本 x j 与 各 个 簇 中 心 μ k 之 间 的 距 离 : d ( x j , μ k ) 2 = ∥ x j − μ k ∥ 2 根 据 距 离 最 近 , 确 定 簇 标 记 λ j = arg min i ∈ 1 , 2 , . . . , K d ( x j , μ k ) 2 将 样 本 划 入 相 应 的 簇 : C λ j = C λ j ∪ x j \begin{aligned}
\boldsymbol{for}& \ j = 1,2,...,m:
\\&计算样本x_j与各个簇中心 \boldsymbol{\mu}_{k} 之间的距离:{d}\left(\boldsymbol{x_j}, \boldsymbol{\mu}_{k}\right)^{2}=\left\|\boldsymbol{x_j}-\boldsymbol{\mu}_{k}\right\|^{2}
\\&根据距离最近,确定簇标记\ \lambda_j = \underset{i\in{1,2,...,K}}{\arg \min} \ {d}\left(\boldsymbol{x_j}, \boldsymbol{\mu}_{k}\right)^{2}
\\&将样本划入相应的簇:C_{\lambda_j}=C_{\lambda_j}\cup{\boldsymbol{x_j}}
\end{aligned}
f o r j = 1 , 2 , . . . , m : 计 算 样 本 x j 与 各 个 簇 中 心 μ k 之 间 的 距 离 : d ( x j , μ k ) 2 = ∥ x j − μ k ∥ 2 根 据 距 离 最 近 , 确 定 簇 标 记 λ j = i ∈ 1 , 2 , . . . , K arg min d ( x j , μ k ) 2 将 样 本 划 入 相 应 的 簇 : C λ j = C λ j ∪ x j
这一步的计算量最大,复杂度 O ( K n p ) O(Knp) O ( K n p )
固定簇成员,对于每个类别,这个时候 i 是固定的。
arg min μ i ∑ j = 1 n m j i ∥ x j − μ i ∥ 2 \underset{\mu_{i}}{\arg \min }\sum_{j=1}^{n} m_{j i}\left\|x_{j}-\mu_{i}\right\|^{2}
μ i arg min j = 1 ∑ n m j i ∥ x j − μ i ∥ 2
找到使SSE最小的 μ i \mu_{i} μ i
求导使得梯度为0,然后求解出μ i \mu_{i} μ i
∑ j = 1 n m j i ( x j − μ i ) = 0 ↓ μ i = ∑ j = 1 n m j i x j ∑ j = 1 n m j i = 1 ∣ C i ∣ ∑ x j ∈ C i x j \sum_{j=1}^{n} m_{j i}(x_{j}-\mu_{i})=0 \\
\downarrow \\
\mu_{i}=\frac{\sum_{j=1}^{n} m_{j i}x_{j}}{\sum_{j=1}^{n} m_{j i}} =\frac{1}{|C_i|}\sum_{x_j \in C_i}{x_j}
j = 1 ∑ n m j i ( x j − μ i ) = 0 ↓ μ i = ∑ j = 1 n m j i ∑ j = 1 n m j i x j = ∣ C i ∣ 1 x j ∈ C i ∑ x j
∑ j = 1 n m j i \sum_{j=1}^{n} m_{j i} ∑ j = 1 n m j i ∣ C i ∣ |C_i| ∣ C i ∣
f o r i = 1 , 2 , . . . , K : 新 的 簇 中 心 : μ i ′ = 1 ∣ C i ∣ ∑ x j ∈ C i x j i f μ i ′ ≠ μ i : 更 新 簇 中 心 : μ i = μ i ′ e l s e μ i ′ ≠ μ i : 保 持 当 前 的 簇 中 心 不 变 \begin{aligned}
\boldsymbol{for}& \ i = 1,2,...,K:
\\ & 新的簇中心:\ \mu'_{i}=\frac{1}{|C_i|}\sum_{x_j \in C_i}{x_j}
\\ &
\boldsymbol{if}\ \mu'_{i} \ne \mu_{i}:\ 更新簇中心:\ \mu_{i}=\mu'_{i}
\\&
\boldsymbol{else}\ \mu'_{i} \ne \mu_{i}:\ 保持当前的簇中心不变
\\
\end{aligned}
f o r i = 1 , 2 , . . . , K : 新 的 簇 中 心 : μ i ′ = ∣ C i ∣ 1 x j ∈ C i ∑ x j i f μ i ′ = μ i : 更 新 簇 中 心 : μ i = μ i ′ e l s e μ i ′ = μ i : 保 持 当 前 的 簇 中 心 不 变
能不能顺序反一下?一开始初始化 C 而不是 μ \mu μ
可以,但更复杂,也没必要。
计算两个 p-维向量之间的欧式距离的复杂度为 O ( p ) O(p) O ( p )
更新簇成员:计算所有点到每个簇中线间的距离,复杂度 O ( K n p ) O(Knp) O ( K n p )
更新簇中心:计算每个簇的簇中心,μ i ′ = 1 ∣ C i ∣ ∑ x j ∈ C i x j \mu'_{i}=\frac{1}{|C_i|}\sum_{x_j \in C_i}{x_j} μ i ′ = ∣ C i ∣ 1 ∑ x j ∈ C i x j O ( n p ) O(np) O ( n p )
假设迭代次数 l l l O ( l K n p ) O(l Knp) O ( l K n p )
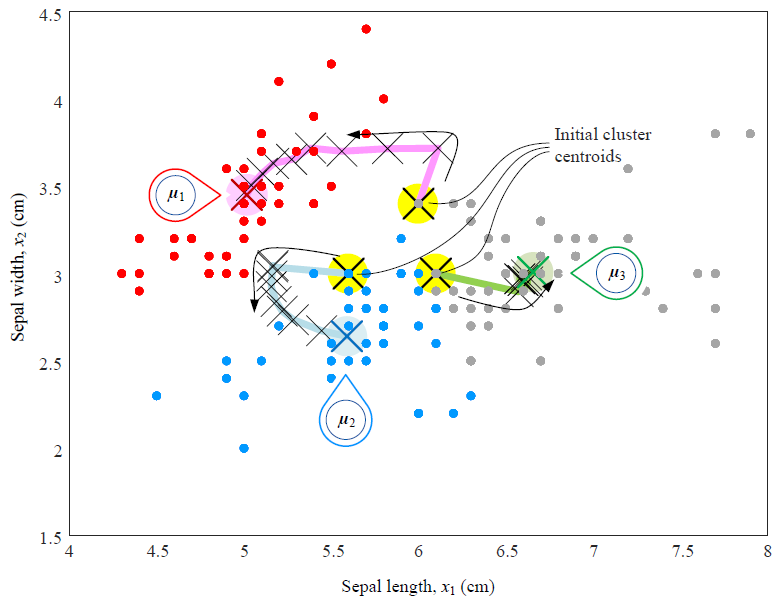
有些初值会导致比较差的结果。
解决办法:
使用启发式方法选择比较好的初值,(例如初值点之间有比较大的距离)、
尝试使用多个初值 选择SSE最小的那一组。
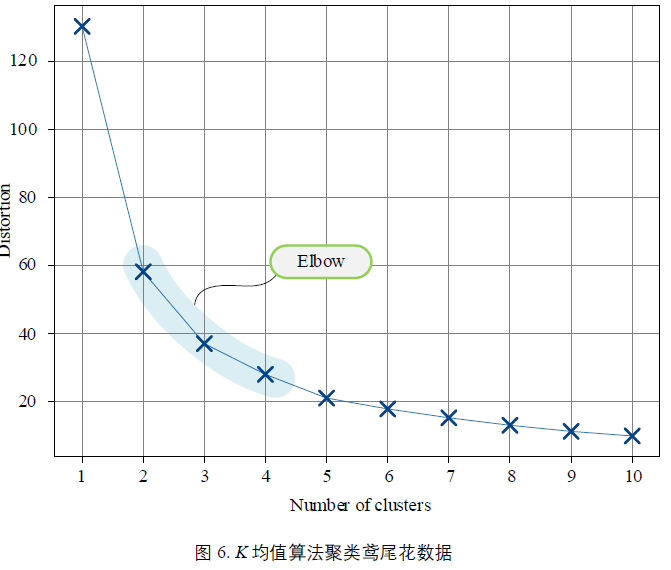
手肘法:
当K 小于 “合适”聚类数时,K 增大时,会导致SSE 大幅下降;但是,K 大于“合适”聚类数时,K 再增大,SSE 下降幅度不断变缓。
所以选择手肘上的 K。(上面这个图中可以选择2,3,4)
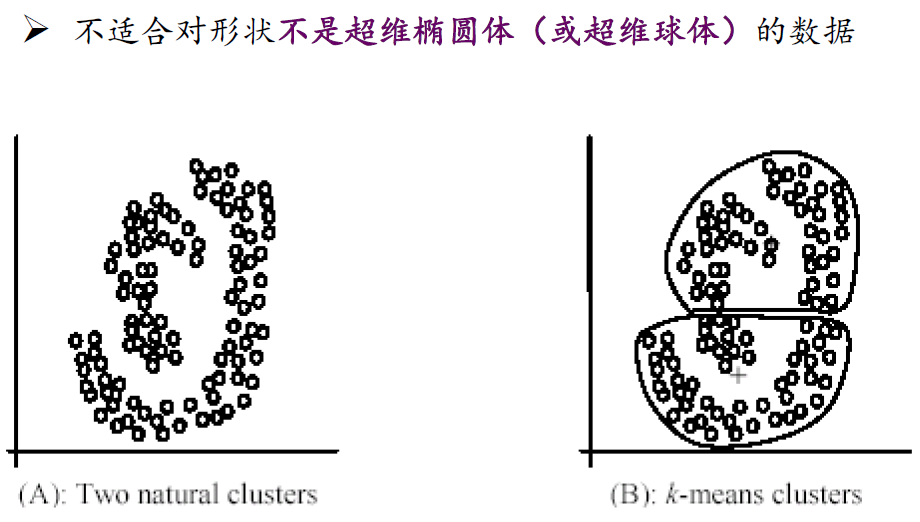
但是实际中,情况可能会更加复杂。
由于 k-means采用距离作为度量,但某些情况下,距离度量不适合划分数据。
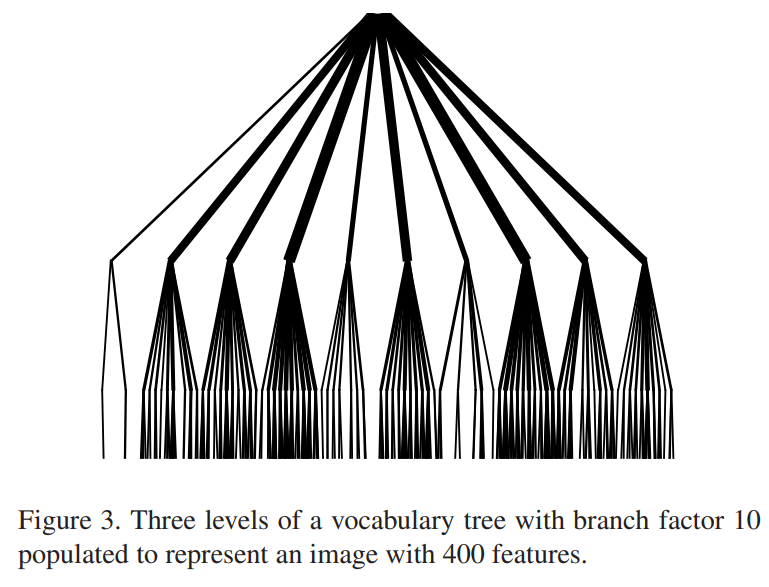
一开始先分成10类,然后每类再分成10类,这样就能迅速达到100类的划分。适合大规模的聚类,每个样本比对的数目可以快速的降低。但是也有问题,前面划分错了,后面就对不回来了。
Nister D, Stewenius H. Scalable recognition with a vocabulary tree[C]//2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06). Ieee, 2006, 2: 2161-2168.
在样本空间上建立一个kd树,利用二分法划分数据。对一个样本计算和簇中心之间的距离的话,就可以在一个小的范围内找,不需要所有簇中心都遍历一遍。
原来是每一个样本 x 要和 K 个簇中心比对。现在是和很少的一部分簇中心比对。也可以做一个大规模的聚类。
Philbin, James, et al. “Object retrieval with large vocabularies and fast spatial matching.” 2007 IEEE conference on computer vision and pattern recognition . IEEE, 2007.
乘积量化 : Product Quantization for Nearest Neighbor Search, PAMI 2011
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 class Kmeans (): def __init__ (self, data, kc, slicesize = 50000 ): """ :param data: shape: (5000404,128) (样本,属性值) :param kc: 中心数量 """ self.slicesize = slicesize self.iter_MAX = 10 self.data = data self.kc = kc self.n = data.shape[0 ] self.d = data.shape[1 ] self.cluster_centers = self.init_cluster_centers() def run (self ): """ 迭代循环 :return: cluster_centers.shape: (kc, 128) """ cluster_centers = self.cluster_centers result_class = np.zeros(self.n) count = 0 while (count <= self.iter_MAX): class_index = self.classify(cluster_centers) if (result_class == class_index).all (): break result_class[:] = class_index cluster_centers = self.new_centers(class_index) count += 1 self.cluster_centers = cluster_centers return cluster_centers def init_cluster_centers (self ): """ 初始化聚类中心,随机选取K个数据点作为簇中心。 :return: cluster_centers.shape: (kc, 128) """ centers = self.data[np.random.choice(np.arange(self.n), self.kc, replace=False )] return centers def classify (self, cluster_centers = None ): """ 根据聚类中心,将样本进行归簇。 :param cluster_centers: :return: shape: (n, ) """ if (cluster_centers is None ): cluster_centers = self.cluster_centers index_list = [] for i in range (0 , self.n, self.slicesize): endi = min (i + self.slicesize, self.n) X = np.repeat(self.data[i: endi, :], self.kc, axis=0 ).reshape((endi-i, self.kc, self.d)) C = np.tile(np.expand_dims(cluster_centers, axis = 0 ), (X.shape[0 ],1 ,1 )) distance = np.sum (np.square(X-C), axis=-1 ) index_list.append(np.argmin(distance, axis=1 )) return np.concatenate(index_list, axis=0 ) def new_centers (self, indexs ): """ 重新计算每个簇的均值,作为新的簇中心。 :param indexs: :return: """ class_sum_list = [[] for _ in range (self.kc)] for i in range (0 , self.n, self.slicesize): endi = min (i + self.slicesize, self.n) for k in range (self.kc): X = self.data[i: endi, :] samples = X[indexs[i: endi]==k] class_sum_list[k].append(np.mean(samples, axis=0 )) return np.mean(class_sum_list, axis=1 )
samples = X[indexs[i: endi]==k]