证据因子可视化
证据因子 :等于三个联合概率的和。
p(x)=k=1∑KJoint p(Ck∩x)
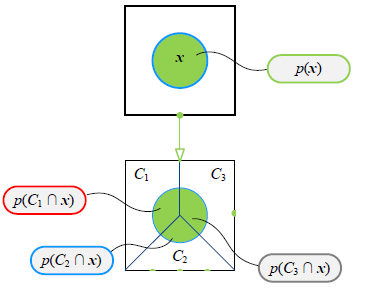
p(x)=k=1∑KJoint p(Ck∩x)=k=1∑K[P(Ck)j=1∏Dp(xj∣Ck)]
比如一个三分类的问题,有三个类别。
p(x)=p(C1∩x)+p(C2∩x)+p(C3∩x)=p(x∣C1)P(C1)+p(x∣C2)P(C2)+p(x∣C3)P(C3)
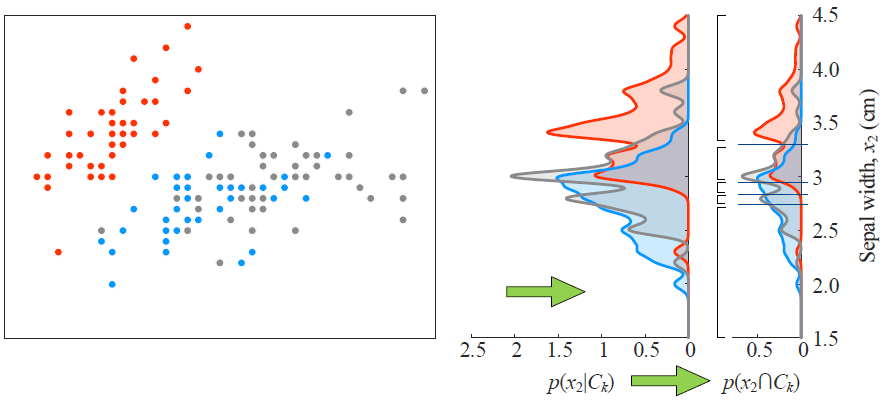
得到三个类别的联合概率(基于KDE核密度估计)
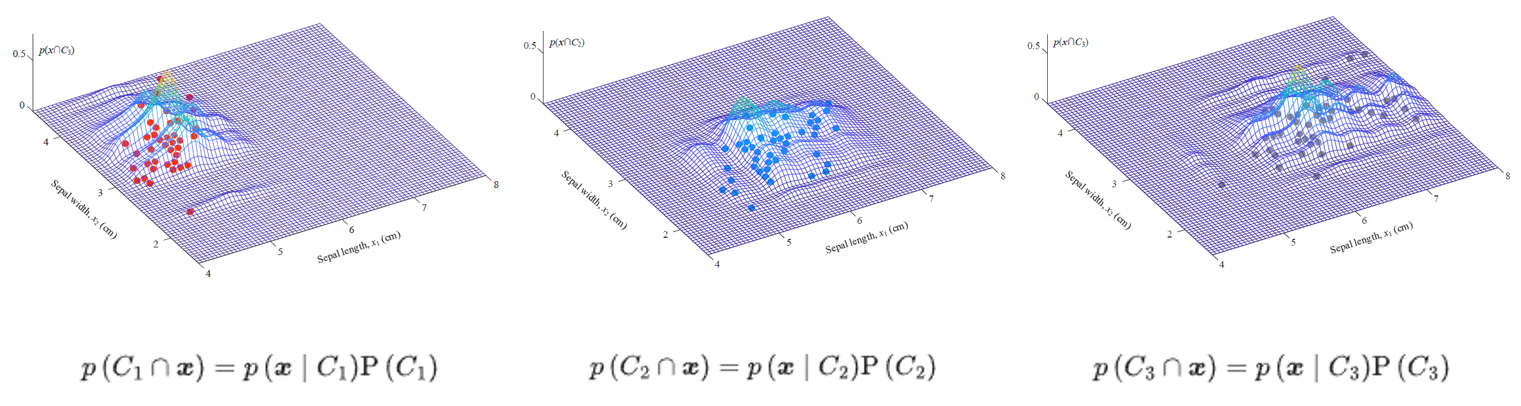
然后把这三个类别的联合概率的曲面相加,就是证据因子。
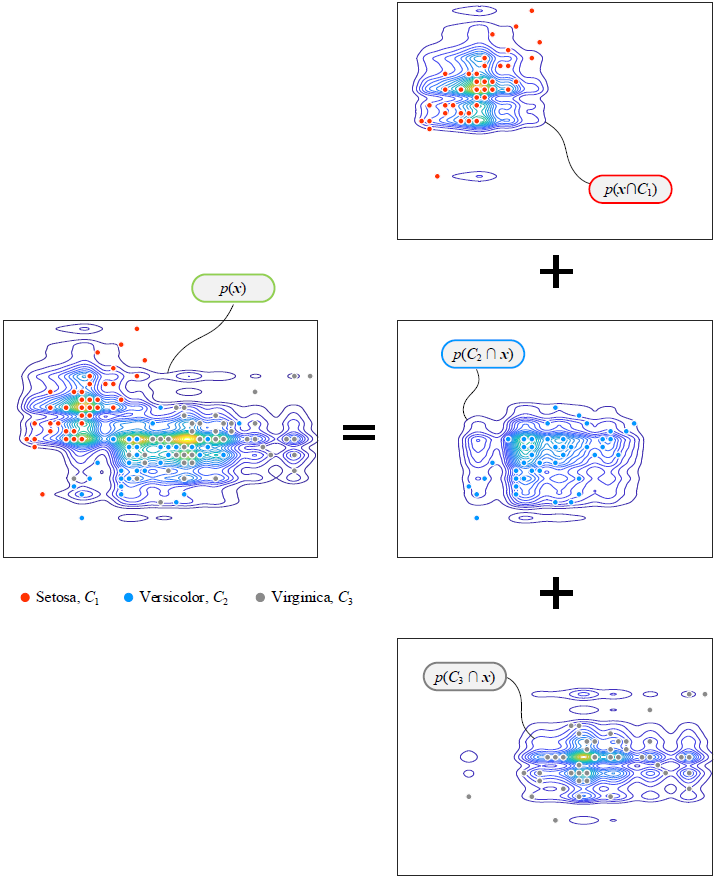
三个联合概率的曲面最后叠加后的证据因子的图像:
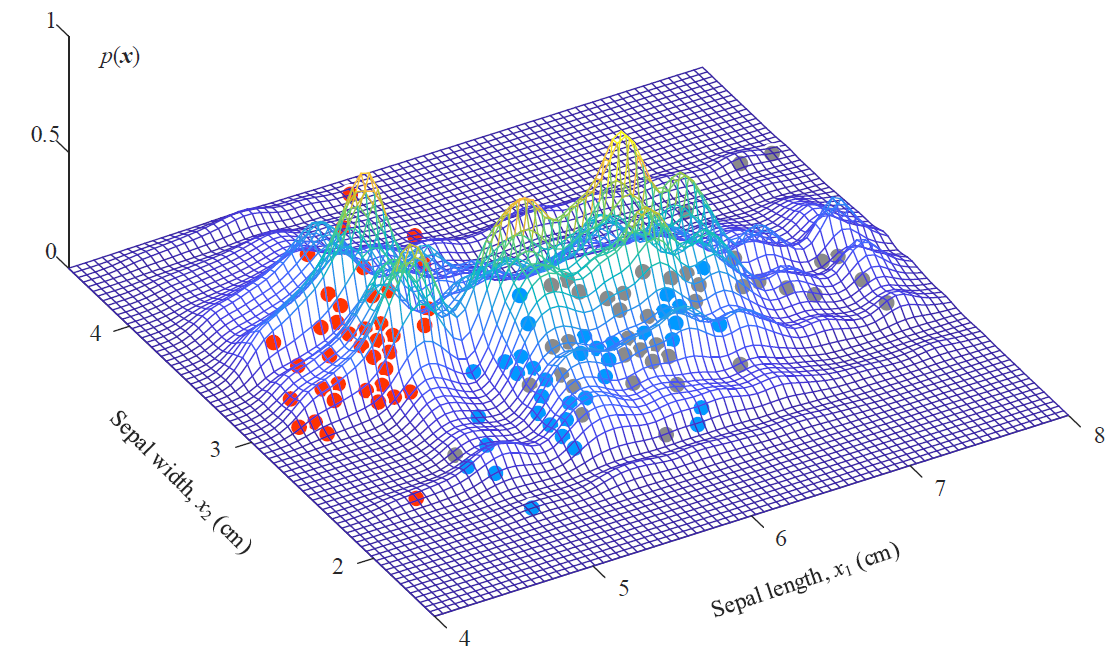
三个颜色的点代表了三个不同的类别。
所以再回头看这个公式:
Posterior p(Ck∣x)=p(x)p(x∩Ck)Joint =Evidencep(x)p(x∣Ck)Likelihood p(Ck)Prior
分子是联合概率,证据因子在分母,与分类无关,起到的是一个归一化的作用(把值调成 (0, 1) 之间)。
这个归一化的时候,分子和分母是相同维度的矩阵,所以做的是一个点除的运算。
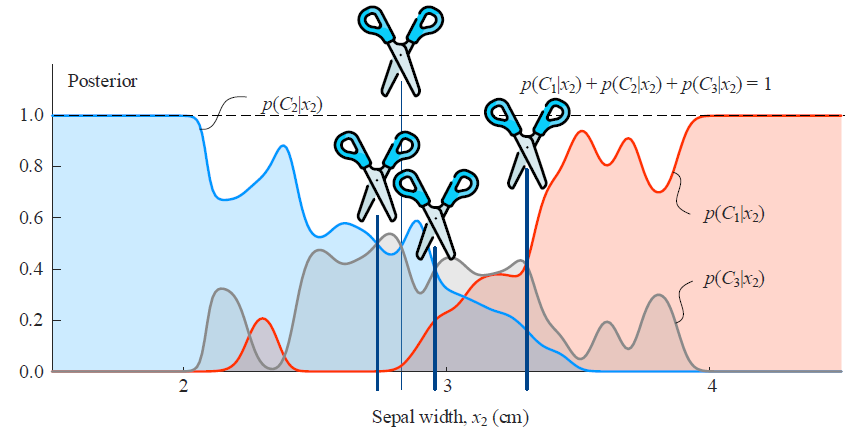
后验概率可视化
经过证据因子的归一化作用,后验概率的相加为1。
Posterior p(Ck∣x)=p(x)p(x∩Ck)Joint
k=1∑KPosterior p(Ck∣x)=1
对于一个三分类的问题:
p(C1∣x)+p(C2∣x)+p(C3∣x)=1
所以后验概率又被称为成员值。
后验的曲面(联合概率曲面归一化后的曲面),比较三个曲面的高度,也可以得到决策边界。(归一化了之后,取值范围是0-1)
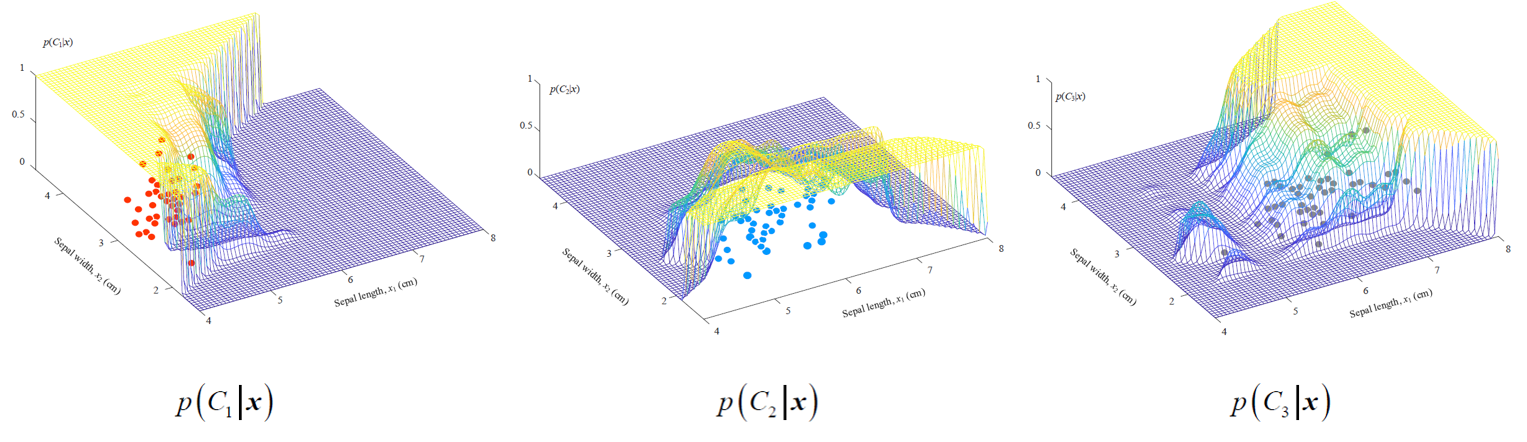
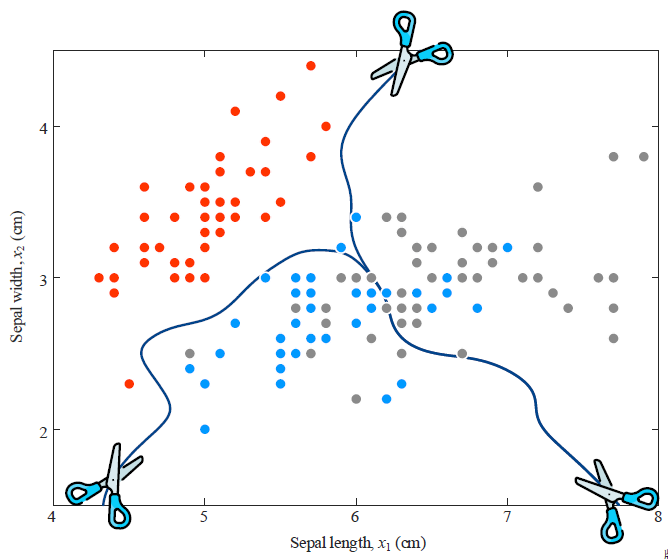
后验概率的可视化效果比较好,因为相比于联合概率,后验概率在 (0, 1) 之间
可视化
可以看b站生姜的原视频,这个可视化非常好!我这里只是想搬运一下他的图。
b站链接 https://www.bilibili.com/video/BV19y4y1L7LQ
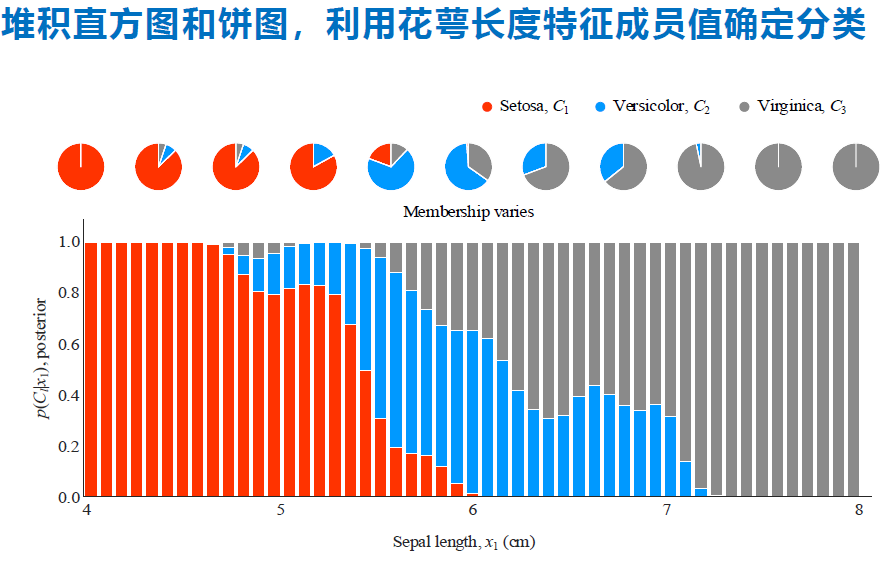
- 似然概率和联合概率,其中某一个属性的可视化结果(花萼长度特征)
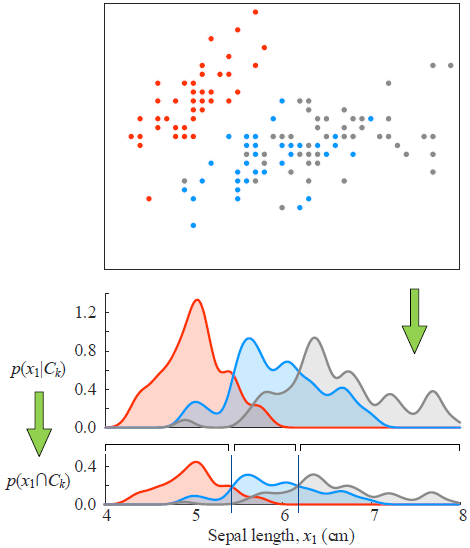
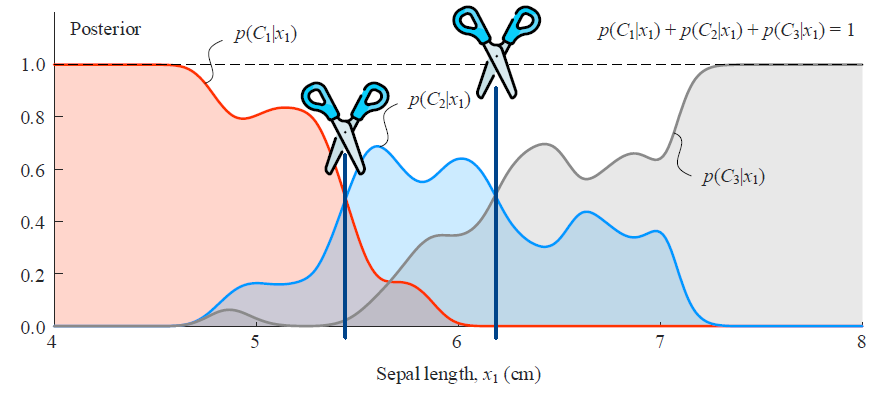
大致就可以分成3类。
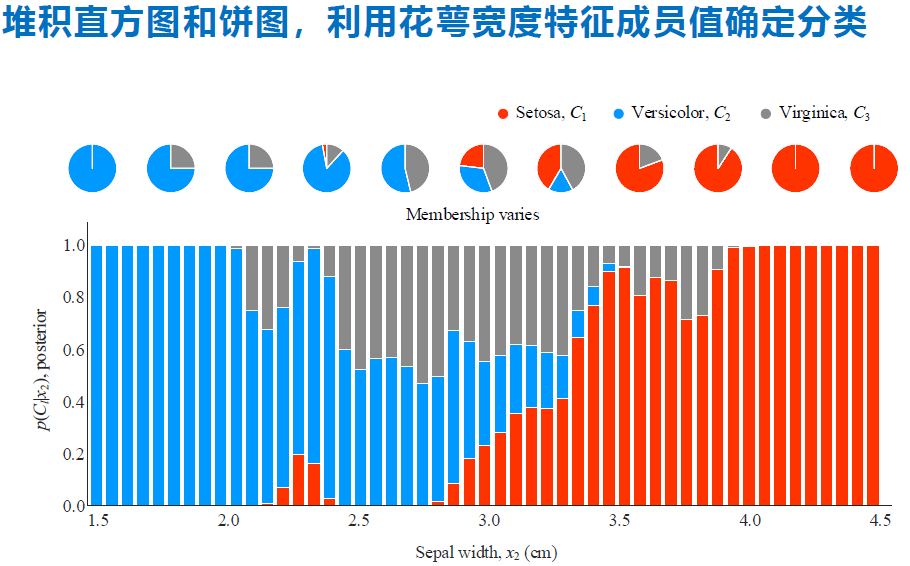
如果从另一个属性来看,是这样的结果。
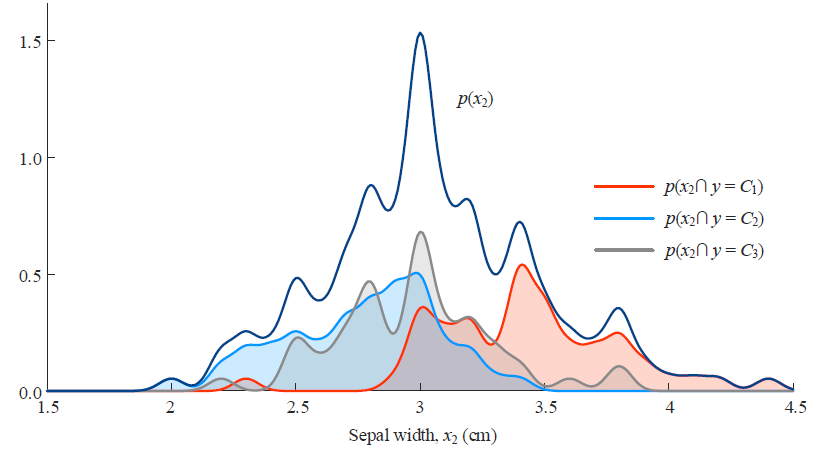
上面这个 p(x2)是证据因子,三个联合概率叠加的结果。
这个直方图效果也很好,可以清除的展示每一个属性值下,成员值(后验概率)的占比情况。
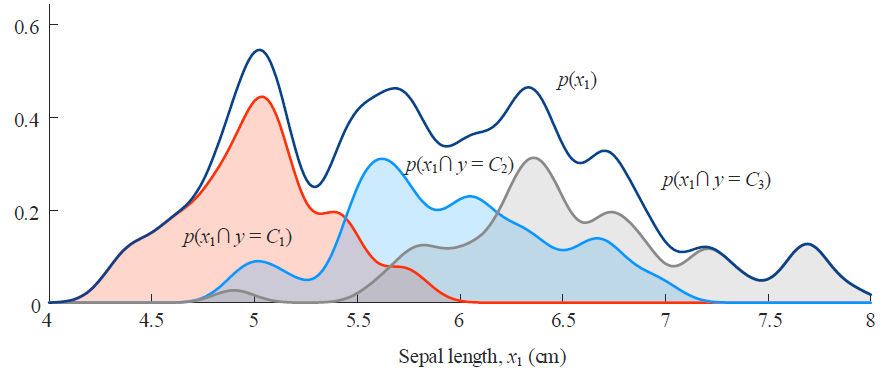
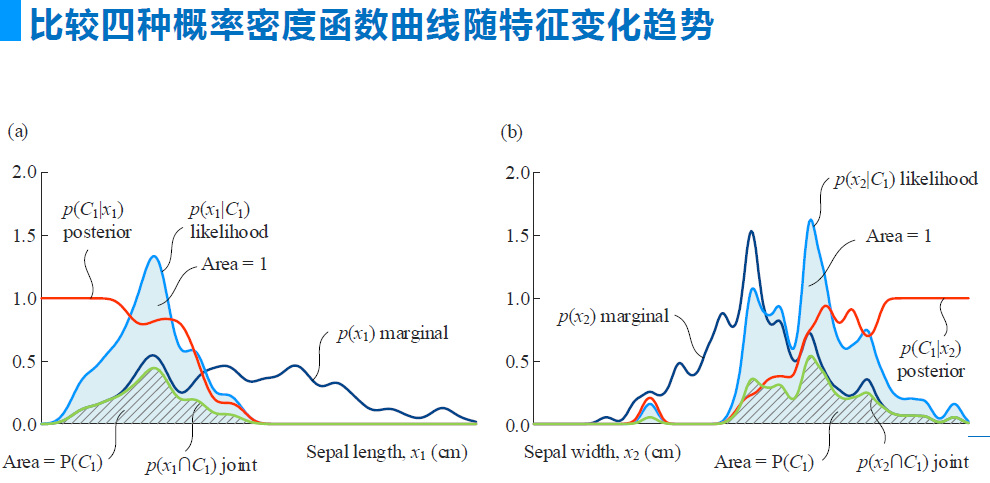
把似然,后验,联合概率,证据因子画在一张图上。(C1类的情况)
似然的面积是1,联合的面积是 P(C1)
reference














