lapt BlogPostsTagsGallerydemogameLeetCode
机器学习-贝叶斯分类笔记(1)
|DL&MLML

贝叶斯公式（似然，先验，后验）↓最大后验概率分类{贝叶斯决策论最大化后验概率等价于期望风险最小化↓最大化后验准则{判别式模型生成式模型↓转化为估计先验P(c)和似然P(x∣c)↓朴素贝叶斯（条件独立性假设）↓朴素贝叶斯的极大似然估计↓贝叶斯估计（包含拉普拉斯平滑）\begin{aligned} &{贝叶斯公式（似然，先验，后验）} \\ &{\downarrow} \\ &{最大后验概率分类 \left\{\begin{matrix}贝叶斯决策论 \\最大化后验概率等价于期望风险最小化 \end{matrix}\right. } \\ &{\downarrow} \\ &最大化后验准则 \left\{\begin{matrix}判别式模型 \\生成式模型 \end{matrix}\right. \\ &{\downarrow} \\ &转化为估计先验P(c)和似然P(x|c) \\ &{\downarrow} \\ &朴素贝叶斯（条件独立性假设） \\ &{\downarrow} \\ & 朴素贝叶斯的极大似然估计\\ &{\downarrow} \\ & 贝叶斯估计 （包含拉普拉斯平滑） \end{aligned}

笔记中符号有些混乱，因为是拷贝了不同的文章和书，凑合着看

贝叶斯公式

针对两个随机变量，联合概率分布有两种分解形式：

P(x,y)=P(x∣y)P(y)=P(y∣x)P(x)P(x, y)=P(x \mid y) P(y)=P(y \mid x) P(x)

贝叶斯公式：

建立了似然概率，先验概率，后验概率之间的联系

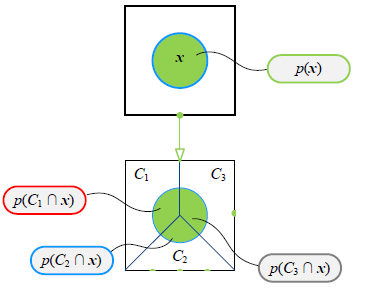
p(Ck∣x)⏟Posterior =p(x∩Ck)⏞Joint p(x)=p(x∣Ck)⏞Likelihood p(Ck)⏞Priorp(x)⏟Evidence\underbrace{p\left(C_{k} \mid \boldsymbol{x}\right)}_{\text {Posterior }}=\frac{\overbrace{p\left(\boldsymbol{x} \cap C_{k}\right)}^{\text {Joint }}}{p(\boldsymbol{x})}=\frac{\overbrace{p\left(\boldsymbol{x} \mid C_{k}\right)}^{\text {Likelihood }} \overbrace{p\left(C_{k}\right)}^{\text {Prior}}}{\underbrace{p(\boldsymbol{x})}_{\text {Evidence}}}

  • p(Ck∣x)p\left(C_{k} \mid \boldsymbol{x}\right) ：后验概率（也叫做成员值 membership score），给定一个样本x\boldsymbol{x}的条件下（观测到x\boldsymbol{x}后），被判定为CkC_{k}类的概率。
  • p(x∣Ck)p\left(\boldsymbol{x} \mid C_{k}\right) ：类条件概率（似然）
  • p(x∩Ck)p\left(\boldsymbol{x} \cap C_{k}\right) ：联合概率
  • p(x)p(\boldsymbol{x}) ：证据因子，用于归一化，与类标记无关，（对于所有的类标记，px都相同）
  • p(Ck)p\left(C_{k}\right) ：类“先验”概率。样本空间中各类样本所占的比例。p(Ck)=count(Ck)count(Ω)=标签是Ck的样本样本空间的集合p\left(C_{k}\right)=\frac{count(C_k)}{count(\Omega )}=\frac{标签是C_k的样本}{样本空间的集合}

一个形象的例子描述

一个三分类问题：

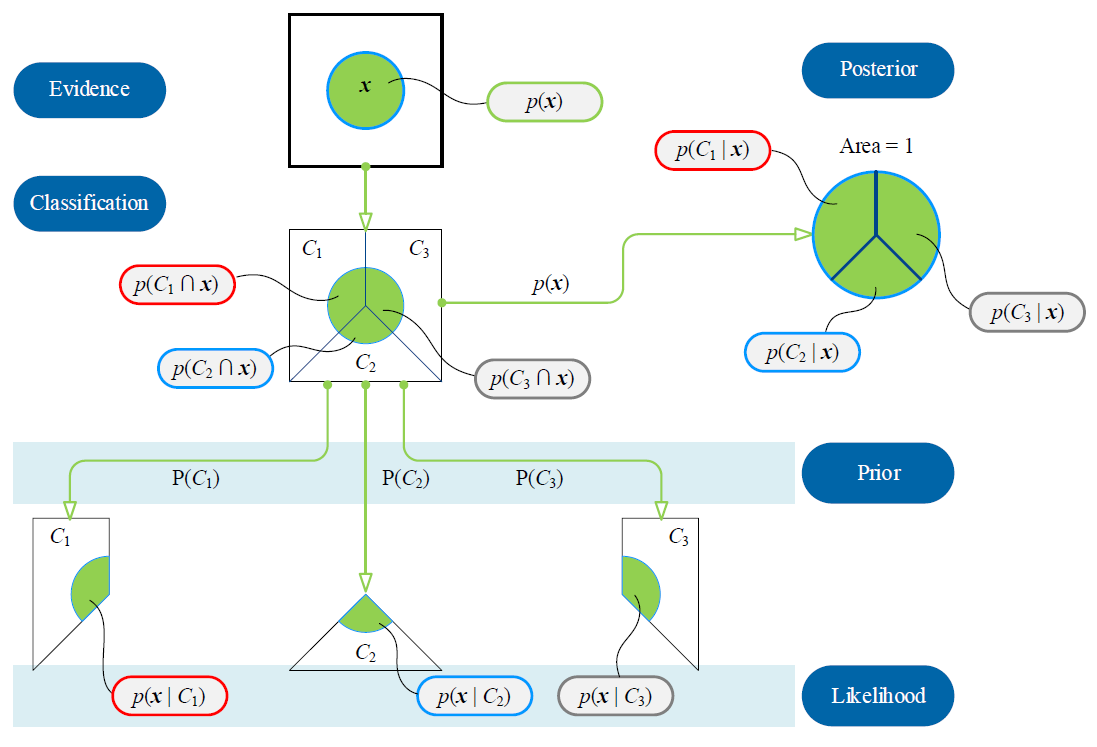
图片来自b站

图片的b站视频链接

其中：

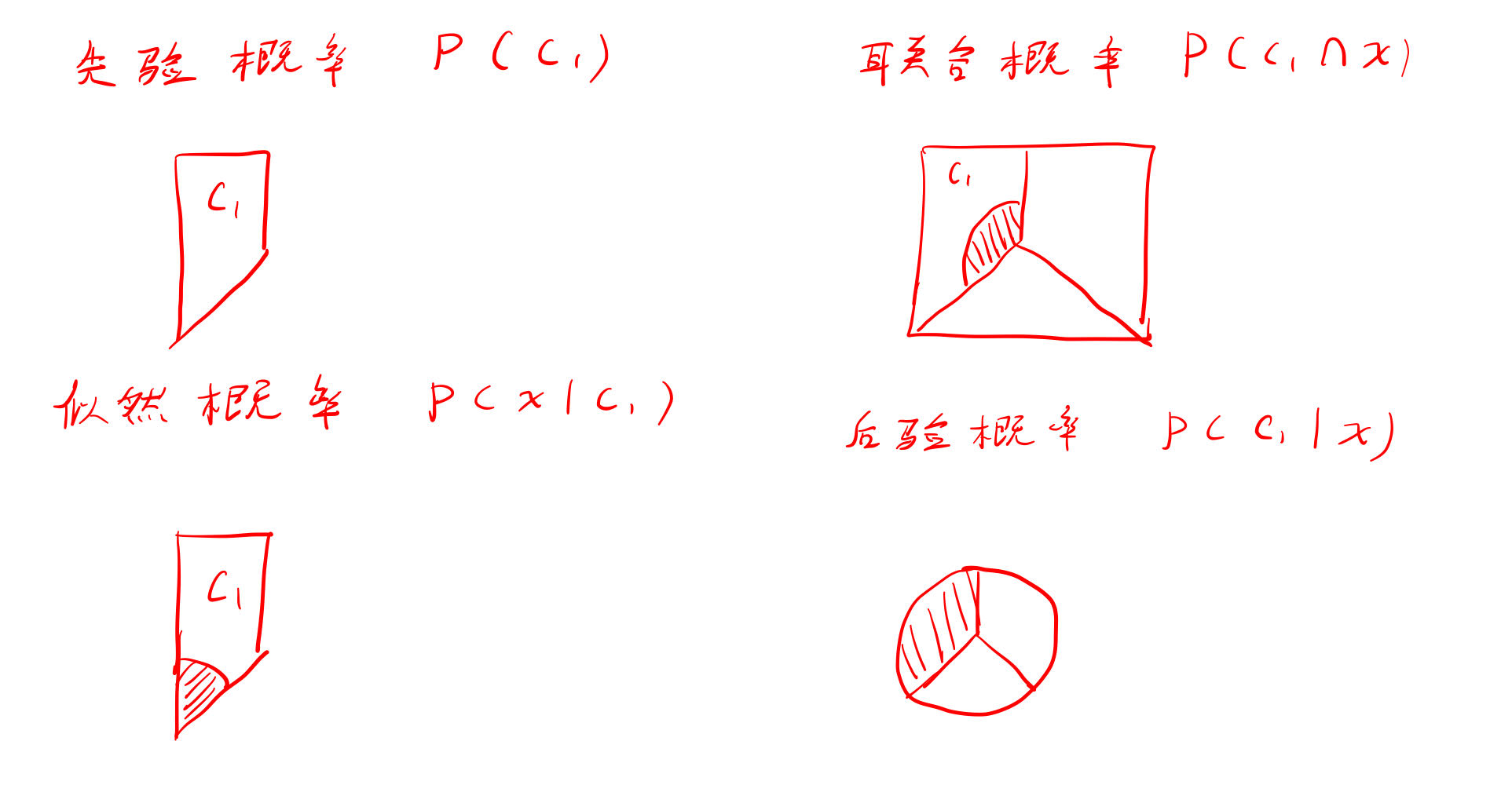
image-20221106162418176

  • 证据因子 ：等于三个联合概率的和。

    p(x)=∑k=1Kp(Ck∩x)⏟Joint p(\boldsymbol{x})=\sum_{k=1}^{K} \underbrace{p\left(C_{k} \cap \boldsymbol{x}\right)}_{\text {Joint }}

    image-20221106162940535

  • 后验概率：

∑k=1Kp(Ck∣x)⏟Posterior =1\sum_{k=1}^{K} \underbrace{p\left(C_{k} \mid \boldsymbol{x}\right)}_{\text {Posterior }}=1

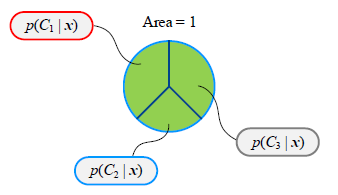
image-20221106162801616

三个类别的后验概率求和为1，所以后验概率也叫做成员值。

​

通过后验概率分类

针对一个二分类问题：

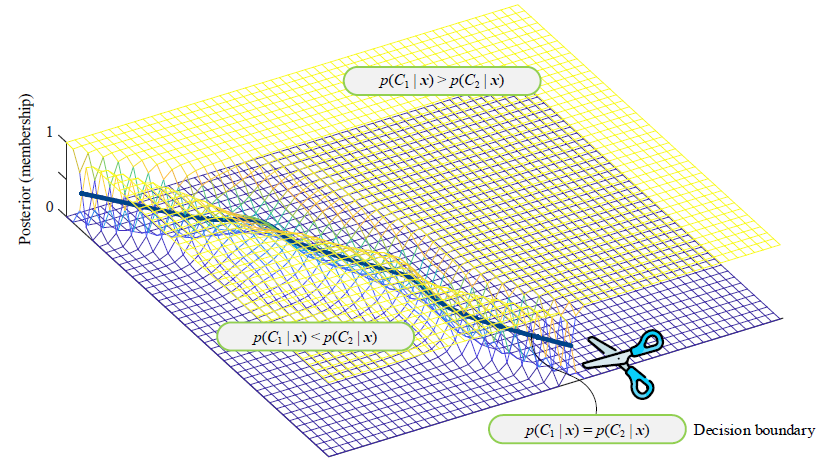
image-20221106163902873

这个图有两个黄色的面，代表了每个点的后验概率，x 是一个二维向量（有两个属性值x1，x2）。

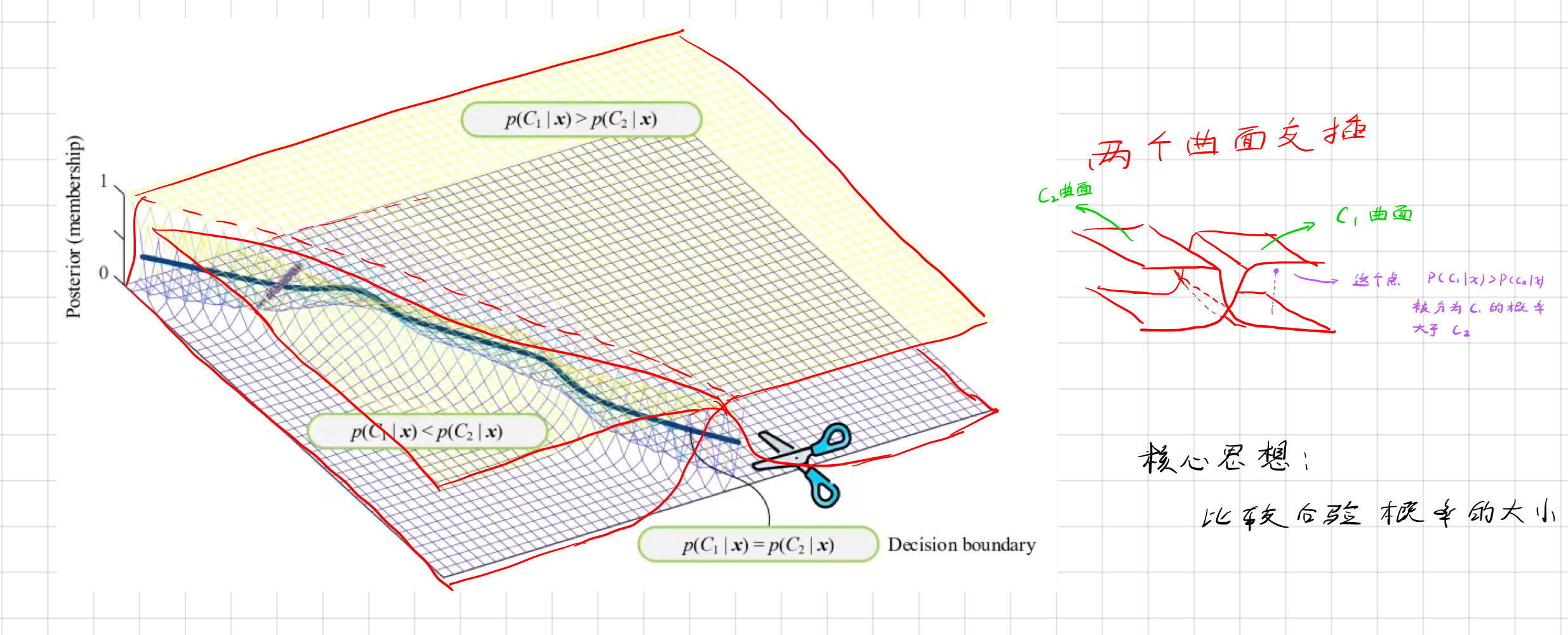
image-20221106164125292

分类的核心思想就是比较后验概率的大小，

对于下面的面，C2的后验概率更大，对于上面的面C1后验概率更大。

最大化后验概率

y^=arg⁡max⁡Ck p(Ck∣x)\hat{y}=\underset{C_{k}}{\arg \max }\ p\left(C_{k} \mid \boldsymbol{x}\right)

找到使后验概率最大的 CkC_{k} 作为预测值。

最大化后验概率的含义

贝叶斯决策论

条件风险

给定样本 x=(x1,…,xp)T\boldsymbol{x}=\left(x_{1}, \ldots, x_{p}\right)^{T} ，基于条件（后验）概率p(Ci∣x)p\left(C_{i} \mid \boldsymbol{x}\right)计算，可获得将样本x\boldsymbol{x}分类为cic_i类所产生的期望损失：

在样本x\boldsymbol{x}上的条件风险：

R(ci∣x)=∑j=1LλijP(cj∣x)R\left(c_{i} \mid \boldsymbol{x}\right)=\sum_{j=1}^{L} \lambda_{i j} P\left(c_{j} \mid \boldsymbol{x}\right)

其中，λij\lambda_{i j}是将一个真实标记为cjc_{j}的样本误分类为cic_{i}所产生的损失：

简化一下就是：

λij={0, if i=j1, otherwise \lambda_{i j}=\left\{\begin{array}{ll} 0, & \text { if } i=j \\ 1, & \text { otherwise } \end{array}\right.

当i=ji=j时，λiiP(ci∣x)=0\lambda_{i i} P\left(c_{i} \mid \boldsymbol{x}\right)=0 是将x\boldsymbol{x}分类到CiC_i类的概率，不应该包括这个概率，（因为我们统计的是分类错误所产生的损失）

贝叶斯最优分类器

最小化分类错误率的贝叶斯最优分类器为：

h∗(x)=arg⁡min⁡c∈Y R(c∣x)h^{*}(x)=\underset{c \in \mathcal{Y} }{\arg \min }\ R(c \mid x)

其中Y={c1,…,cN}\mathcal{Y}=\left \{c_{1}, \ldots, c_{N} \right\} 表示N个类别标记。

最大化后验概率等价于期望风险最小化

∑iNP(ci∣x)=1↓R(ci∣x)=∑j=1LλijP(cj∣x)=1−P(ci∣x)↓h∗(x)=arg⁡min⁡c∈Y R(c∣x) ⟶ h∗(x)=arg⁡max⁡c∈Y P(c∣x)Y={c1,…,cN}\sum_{i}^{N}{P\left(c_{i} \mid \boldsymbol{x}\right)}=1 \\ \downarrow \\ R\left(c_{i} \mid \boldsymbol{x}\right)=\sum_{j=1}^{L} \lambda_{i j} P\left(c_{j} \mid \boldsymbol{x}\right)=1-P\left(c_{i} \mid \boldsymbol{x}\right) \\ \downarrow \\ h^{*}(x)=\underset{c \in \mathcal{Y} }{\arg \min }\ R(c \mid x) \ \longrightarrow \ h^{*}(x)=\underset{c \in \mathcal{Y} }{\arg \max }\ P(c\mid x) \\ \mathcal{Y}=\left \{c_{1}, \ldots, c_{N} \right\}

或者换个符号解释：

h∗(x)=arg⁡min⁡y∈Y∑k=1KP(y≠ck∣X=x)=arg⁡min⁡y∈Y (1−P(y=ck∣X=x))=arg⁡max⁡y∈Y P(y=ck∣X=x)\begin{aligned} h^{*}(x)&=\underset{y \in \mathcal{Y} }{\arg \min }\sum_{k=1}^{K}{P(y\ne c_k | X=x)} \\ &=\underset{y \in \mathcal{Y} }{\arg \min }\ (1-P(y = c_k | X=x)) \\ &=\underset{y \in \mathcal{Y} }{\arg \max }\ P(y = c_k | X=x) \end{aligned}

总之，最大化后验概率等价于期望风险最小化。

h∗(x)=arg⁡min⁡c∈Y R(c∣x)⏟条件风险↓h∗(x)=arg⁡max⁡c∈Y P(c∣x)⏟后验概率h^{*}(x)=\underset{c \in \mathcal{Y} }{\arg \min }\ \underbrace{R(c \mid x)}_{\text 条件风险} \\ \downarrow \\ h^{*}(x)=\underset{c \in \mathcal{Y} }{\arg \max }\ \underbrace{P(c\mid x)}_{\text 后验概率}

最大后验准则 MAP

我们想要通过最大化后验概率（找到使后验概率P(c∣x)P(c\mid x)最大的cc），但是在现实任务中，后验概率不好获得，从这个角度看，机器学习所要实现的是基于有限的训练样本集尽可能准确地估计出后验概率。

主要有两种策略（判别式、生成式）：

判别式模型

给定x\boldsymbol{x}，直接对P(c∣x)P(c\mid x)进行建模来预测c。这样得到的就是判别器模型。

一个例子是逻辑回归：

P(c∣x;θ)=(fθ(x))c(1−fθ(x))1−cc∈{0,1}fθ(x)=11+e−θTx\begin{array}{l} P(c \mid x ; \theta)=\left(f_{\theta}(x)\right)^{c}\left(1-f_{\theta}(x)\right)^{1-c} \\ c \in\{0,1\}\\ f_{\theta}(x)=\frac{1}{1+e^{-\theta^{T} x}} \end{array}

直接是通过数据集训练了一个判别式概率分类器，输入是 x，输出是多个类别的后验概率。

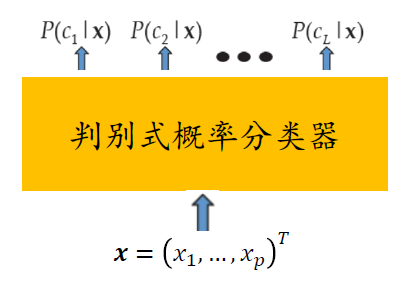
image-20221106192908860

生成式模型

假定类条件概率具有某种确定的概率分布。先对联合概率分布P(x,c)P(x,c)建模，再通过贝叶斯公式计算后验概率P(c∣x)P(c|x)

根据贝叶斯定理：

p(Ck∣x)⏟Posterior =p(x∩Ck)⏞Joint p(x)=p(x∣Ck)⏞Likelihood p(Ck)⏞Priorp(x)⏟Evidence\underbrace{p\left(C_{k} \mid \boldsymbol{x}\right)}_{\text {Posterior }}=\frac{\overbrace{p\left(\boldsymbol{x} \cap C_{k}\right)}^{\text {Joint }}}{p(\boldsymbol{x})}=\frac{\overbrace{p\left(\boldsymbol{x} \mid C_{k}\right)}^{\text {Likelihood }} \overbrace{p\left(C_{k}\right)}^{\text {Prior}}}{\underbrace{p(\boldsymbol{x})}_{\text {Evidence}}}

其中，p(x)p(\boldsymbol{x})是证据因子，对所有类别都一样，也就说，分母一样，所以后验概率正比于联合概率：

p(Ck∣x)∝p(Ck∩x)p\left(C_{k} \mid \boldsymbol{x}\right) \propto p\left(C_{k} \cap \boldsymbol{x}\right)

最大化后验概率，等价于最大化联合概率。

arg⁡max⁡c∈Y P(c∣x) ⟶ arg⁡max⁡c∈Y P(c∩x)\underset{c \in \mathcal{Y} }{\arg \max }\ P(c\mid x) \ \longrightarrow \ \underset{c \in \mathcal{Y} }{\arg \max }\ P(c \cap x)

最终，估计后验概率的问题就转化成了基于训练数据D来估计先验P(c)P(c)和似然P(x∣Ck)P(\boldsymbol{x} \mid C_{k})

argmax⁡CiP(Ci∣X)=argmax⁡ciP(X,Ci)⏞联合=argmax⁡P(X∣Ci)⏞类条件P(Ci)⏞先验\underset{C_{i}}{\operatorname{argmax}} P\left(C_{i} \mid X\right)=\underset{c_{i}}{\operatorname{argmax}} \overbrace{P\left(X, C_{i}\right)}^{\text 联合}=\operatorname{argmax} \overbrace{P\left(X \mid C_{i}\right)}^{\text 类条件} \overbrace{P\left(C_{i}\right)}^{先验}

朴素贝叶斯

通过生成模型，估计后验概率的问题就转化成了基于训练数据D来估计先验P(c)P(c)和似然P(x∣Ck)P(\boldsymbol{x} \mid C_{k})。P(c)P(c)好说，但是想要估计P(x∣Ck)P(\boldsymbol{x} \mid C_{k}) 还是比较难，

argmax⁡cj∈CP(x1,x2,…,xp∣cj)P(cj)\underset{c_{j} \in C}{\operatorname{argmax}} P\left(x_{1}, x_{2}, \ldots, x_{p} \mid c_{j}\right) P\left(c_{j}\right)

需要太多的参数，假设x(j)x^{(j)}的可能取值有SjS_j个，j=1,2,...,nj=1,2,...,n，YY的取值有K个，则参数的个数为 K∏j=1nSjK \prod_{j=1}^{n}S_j。

比如说假设样本有p个属性，每个属性有d种可能，则共需要dpd^p个条件概率。

比如说，能不能去打网球得看 x(1)x^{(1)}天气(晴天，大风，雨天) 和 x(2)x^{(2)}温度（高，中，低）这两个属性，每个属性可能取值都是3个，那么一共有2*3*3种不同的天气和温度的组合。而如果使用贝叶斯，我们只需要估计2*(3+3)个条件概率。

朴素贝叶斯做了一个假设（属性条件独立性假设），对已知类别，假设所有的属性相互独立。

  • 原本的条件概率分布：

P(X=x∣Y=ck)=P(X(1)=x(1),⋯ ,X(n)=x(n)∣Y=ck),k=1,2,⋯ ,KP\left(X=x \mid Y=c_{k}\right)=P\left(X^{(1)}=x^{(1)}, \cdots, X^{(n)}=x^{(n)} \mid Y=c_{k}\right), k=1,2, \cdots, K

  • 条件独立性假设：

P(X=x∣Y=ck)=P(X(1)=x(1),⋯ ,X(n)=x(n)∣Y=ck)=∏j=1nP(X(j)=x(j)∣Y=ck)\begin{aligned} P\left(X=x \mid Y=c_{k}\right) &=P\left(X^{(1)}=x^{(1)}, \cdots, X^{(n)}=x^{(n)} \mid Y=c_{k}\right) \\ &=\prod_{j=1}^{n} P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right) \end{aligned}

  • 在属性条件独立的假设下，联合概率计算式为：

p(Ck∩x)=p(x∣Ck)P(Ck)=P(Ck)∏j=1Dp(xj∣Ck)p\left(C_{k} \cap \boldsymbol{x}\right)=p\left(\boldsymbol{x} \mid C_{k}\right) \mathrm{P}\left(C_{k}\right)=\mathrm{P}\left(C_{k}\right) \prod_{j=1}^{D} p\left(x_{j} \mid C_{k}\right)

注意这个是属性条件独立性假设，有条件的。不是属性独立。得给定 c 这个条件（已知类别）才能成立

属性条件独立不能推广到属性独立，反过来也一样。

  • 因此：

h∗(x)=arg⁡max⁡cj∈CP(cj)P(x∣cj)↓h∗(x)=arg⁡max⁡cj∈CP(cj)∏i=1PP(xi∣cj)\begin{aligned} h^{*}(x)&=\arg \max _{c_{j} \in C} {P\left(c_{j}\right)} {P\left( \boldsymbol{x}\mid c_{j}\right)} \\ \downarrow \\ h^{*}(x)&=\arg \max _{c_{j} \in C} P\left(c_{j}\right) \prod_{i=1}^{P} P\left(x_{i} \mid c_{j}\right) \end{aligned}

就可以对每一个不同的属性进行分别的研究/计算。

这样，比如说假设样本有p个属性，每个属性有d钟可能，则共需要dp个条件概率。（从dpd^p讲到dp）

朴素贝叶斯的极大似然估计

在朴素贝叶斯法中，概率模型的训练过程就是估计 P(Y=ck)P\left(Y=c_{k}\right) 和 P(X=x∣Y=ck)P\left(X=x \mid Y=c_{k}\right)。

应用极大似然估计法估计相应的概率：

先验概率的极大似然估计

P(Y=ck)=∑i=1NI(yi=ck)N,k=1,2,⋯ ,KP\left(Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)}{N}, \quad k=1,2, \cdots, K

II为指示函数，当yi=cky_{i}=c_{k}成立时，I(yi=ck)=1I\left(y_{i}=c_{k}\right)=1，否则是0

也就是该类样本占总样本的比例。

条件概率的极大似然估计

设第j个特征x(j)x^{(j)}的可能取值是{aj1,aj2,⋯ ,ajSj}\left\{a_{j 1}, a_{j 2}, \cdots, a_{j S_{j}}\right\}，条件概率 P(X(j)=ajl∣Y=ck)P\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)的极大似然估计为：

P(X(j)=ajl∣Y=ck)=∑i=1NI(xi(j)=ajl,yi=ck)∑i=1NI(yi=ck) j=1,2,⋯ ,n;l=1,2,⋯ ,Sj;k=1,2,⋯ ,KP\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j l}, y_{i}=c_{k}\right)}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)} \\ \ \\ j=1,2, \cdots, n ; \quad l=1,2, \cdots, S_{j} ; \quad k=1,2, \cdots, K

其中，xi(j)x_{i}^{(j)}是第i个样本的第j个特征，ajla_{j l}是第j个特征可能取的第ll个值，II为指示函数。

II为指示函数，当yi=cky_{i}=c_{k}成立时，I(yi=ck)=1I\left(y_{i}=c_{k}\right)=1，否则是0

也就是，有该属性的某个值且为ck的样本数占ck的样本总数。

贝叶斯估计（拉普拉斯平滑）

用极大似然估计可能会出现所要估计的概率为0的情况。比如某个属性值在训练集中没有在某个类中出现过，在连乘的时候，也会抹去其他的属性信息。

也就是说：当∑i=1NI(xi(j)=ajl,yi=ck)=0\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j l}, y_{i}=c_{k}\right)=0 时候：

P(X(j)=ajl∣Y=ck)=∑i=1NI(xi(j)=ajl,yi=ck)∑i=1NI(yi=ck)=0∑i=1NI(yi=ck)=0P\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j l}, y_{i}=c_{k}\right)}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)} =\frac{0}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)}=0

这种情况可能是，并没有xi(j)=ajlx_{i}^{(j)}=a_{j l} 且yi=cky_{i}=c_{k}的样本。所以分子是0

为了避免这个情况出现，我们采用贝叶斯估计的方法（避免出现0的情况）：

条件概率的贝叶斯估计

Pλ(X(j)=ajl∣Y=ck)=∑i=1NI(xi(j)=ajt,yi=ck)+λ∑i=1NI(yi=ck)+SjλP_{\lambda}\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j t}, y_{i}=c_{k}\right)+\lambda}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)+S_{j} \lambda}

当λ=1\lambda=1时，为拉普拉斯平滑。SjS_{j}是第jj个特征x(j)x^{(j)}的属性的取值个数。（第j个特征x(j)x^{(j)}的可能取值是{aj1,aj2,⋯ ,ajSj}\left\{a_{j 1}, a_{j 2}, \cdots, a_{j S_{j}}\right\}）

先验概率的贝叶斯估计

Pλ(Y=ck)=∑i=1NI(yi=ck)+λN+KλP_{\lambda}\left(Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)+\lambda}{N+K \lambda}

Y的可能取值有K个（类的个数）。N是训练集的数据个数。

应用

通过数据集的训练，我们估计出了条件概率 P(x∣cj)P\left( \boldsymbol{x}\mid c_{j}\right) 和 P(cj)P\left(c_{j}\right) 先验概率

比如说对于那个贝叶斯文本分类的任务来说，每一个词可以看作是一个属性，那么字典的长度就是属性的可能取值的个数，估计出的 P(x∣cj)P\left( \boldsymbol{x}\mid c_{j}\right) 是一个维度为（字典长度 * 文档类别）。P(cj)P\left(c_{j}\right) 就是 （文档类别的一个一维向量）

然后测试的时候，计算

arg⁡max⁡cj∈CP(cj)∏i=1PP(xi∣cj)\arg \max _{c_{j} \in C} P\left(c_{j}\right) \prod_{i=1}^{P} P\left(x_{i} \mid c_{j}\right)

程序中连乘容易趋于0，于是采用 ln 加和的形式。

ctext=argmax⁡c∈C[ln⁡P(c)+∑i=1nln⁡P(wi∣c)]c_{t e x t}=\operatorname{argmax}_{c \in C}\left[\ln P(c)+\sum_{i=1}^{n} \ln P\left(w_{i} \mid c\right)\right]

比如说，每个词是一个属性吧，每一个词在文档中出现的次数作为属性值，那么出现一次，就加一次 ln⁡P(wi∣c)\ln P\left(w_{i} \mid c\right)

wi 表示的是某个词的条件概率

DL&ML