使用软间隔SVM在给定的数据集上进行训练和测试。
使用佩加索斯(Pegasos)算法近似求解SVM的目标函数。
代码思路:
数据读取:读取 train 数据集和 test 数据集 (测试集样本数:1000;训练集样本数:4000)
1 2 3 4 train_x = train['X' ] train_y = train['y' ] test_x = test['Xtest' ] test_y = test['ytest' ]
计算 lambda:lambda_ = 1 / (num_train * C) 其中num_train是样本数量,C是惩罚参数。
初始化权重W和偏置b:
1 2 W = np.random.randn(num_features, 1 ) b = np.random.randn(1 )
使用佩加索斯算法,每次随机挑选一个样本进行参数估计:
使用 hinge损失
使用 指数损失
使用 对率损失
不断重复更新过程,直到循环结束。
计算准确率,画出目标函数曲线。
软间隔支持向量机引入松弛变量,优化问题为:
min w , b w T w / 2 + C ∑ i = 1 n ϵ i s . t . y i ( w T x i + b ) ≥ 1 − ϵ i ϵ i ≥ 0 \begin{aligned}
& \min _{w, b} w^{T} w / 2+C \sum_{i=1}^{n} \epsilon_{i} \\
s.t. \quad
& y_{i}\left(w^{T} x_{i}+b\right) \geq 1-\epsilon_{i} \\
& \epsilon_{i} \geq 0
\end{aligned}
s . t . w , b min w T w / 2 + C i = 1 ∑ n ϵ i y i ( w T x i + b ) ≥ 1 − ϵ i ϵ i ≥ 0
利用hinge损失可以对松弛变量做更巧妙的表达:
ϵ i = { 0 , if y i ( w T x i + b ) ≥ 1 1 − y i ( w T x i + b ) , if y i ( w T x i + b ) < 1 \epsilon_{i}=\left\{\begin{array}{ll}
0, & \text { if } y_{i}\left(w^{T} x_{i}+b\right) \geq 1 \\
1-y_{i}\left(w^{T} x_{i}+b\right), & \text { if } y_{i}\left(w^{T} x_{i}+b\right)<1
\end{array}\right.
ϵ i = { 0 , 1 − y i ( w T x i + b ) , if y i ( w T x i + b ) ≥ 1 if y i ( w T x i + b ) < 1
目标函数变为(更一般的形式 $ C = \frac{1}{n\lambda} $) :
min w , b f ( w , b ) = λ 2 ∥ w ∥ 2 + 1 n ∑ i = 1 n max ( 0 , 1 − y i ( w T x i + b ) ) \min _{w, b} f(w, b)=\frac{\lambda}{2}\|w\|^{2}+\frac{1}{n} \sum_{i=1}^{n} \max \left(0,1-y_{i}\left(w^{T} x_{i}+b\right)\right)
w , b min f ( w , b ) = 2 λ ∥ w ∥ 2 + n 1 i = 1 ∑ n max ( 0 , 1 − y i ( w T x i + b ) )
随机选择一个样本点的目标函数:
f ( w , b ) = λ 2 ∥ w ∥ 2 + max ( 0 , 1 − y i ( w T x i + b ) ) f(w, b)=\frac{\lambda}{2}\|w\|^{2}+\max \left(0,1-y_{i}\left(w^{T} x_{i}+b\right)\right)
f ( w , b ) = 2 λ ∥ w ∥ 2 + max ( 0 , 1 − y i ( w T x i + b ) )
分别对w和b求偏导,然后更新参数 w和b:
[ w t + 1 b t + 1 ] = [ w t b t ] − η t [ ∂ f ∂ w ∂ f ∂ b ] \left[\begin{array}{l}
w_{t+1} \\
b_{t+1}
\end{array}\right]=\left[\begin{array}{l}
w_{t} \\
b_{t}
\end{array}\right]-\eta_{t}\left[\begin{array}{c}
\frac{\partial f}{\partial w} \\
\frac{\partial f}{\partial b}
\end{array}\right]
[ w t + 1 b t + 1 ] = [ w t b t ] − η t [ ∂ w ∂ f ∂ b ∂ f ]
hinge 损失: ℓ hinge ( z ) = max ( 0 , 1 − z ) \ell_{\text {hinge }}(z)=\max (0,1-z) ℓ hinge ( z ) = max ( 0 , 1 − z )
因为Hinge损失并非处处可导,所以需要情况讨论:
若 y i ( w T x i + b ) < 1 y_{i}\left(w^{T} x_{i}+b\right)<1 y i ( w T x i + b ) < 1
目标函数: f ( w , b ) = λ 2 ∥ w ∥ 2 + max ( 0 , 1 − y i ( w T x i + b ) ) f(w, b)=\frac{\lambda}{2}\|w\|^{2}+\max \left(0,1-y_{i}\left(w^{T} x_{i}+b\right)\right) f ( w , b ) = 2 λ ∥ w ∥ 2 + max ( 0 , 1 − y i ( w T x i + b ) )
对 w 求偏导: ∂ f ∂ w = λ w − y i x i \frac{\partial f}{\partial w} = \lambda w-y_i x_i ∂ w ∂ f = λ w − y i x i
对 b 求偏导: $\frac{\partial f}{\partial b} = -y_i $
若 y i ( w T x i + b ) ≥ 1 y_{i}\left(w^{T} x_{i}+b\right) \ge 1 y i ( w T x i + b ) ≥ 1
目标函数: f ( w , b ) = λ 2 ∥ w ∥ 2 f(w, b)=\frac{\lambda}{2}\|w\|^{2} f ( w , b ) = 2 λ ∥ w ∥ 2
对 w 求偏导: ∂ f ∂ w = λ w \frac{\partial f}{\partial w} = \lambda w ∂ w ∂ f = λ w
对 b 求偏导: $\frac{\partial f}{\partial b} = 0 $
指数损失: ℓ exp ( z ) = exp ( − z ) \ell_{\text {exp}}(z)=\exp(-z) ℓ exp ( z ) = exp ( − z )
目标函数: f ( w , b ) = λ 2 ∥ w ∥ 2 + exp ( − y i ( w T x i + b ) ) f(w, b)=\frac{\lambda}{2}\|w\|^{2}+\exp(-y_{i}\left(w^{T} x_{i}+b\right)) f ( w , b ) = 2 λ ∥ w ∥ 2 + exp ( − y i ( w T x i + b ) )
对 w 求偏导: ∂ f ∂ w = λ w − y i x i exp ( − y i ( w T x i + b ) ) \frac{\partial f}{\partial w} = \lambda w-y_i x_i \exp(-y_{i}\left(w^{T} x_{i}+b\right)) ∂ w ∂ f = λ w − y i x i exp ( − y i ( w T x i + b ) )
对 b 求偏导: ∂ f ∂ b = − y i exp ( − y i ( w T x i + b ) ) \frac{\partial f}{\partial b} = -y_i \exp(-y_{i}\left(w^{T} x_{i}+b\right)) ∂ b ∂ f = − y i exp ( − y i ( w T x i + b ) )
指数损失: ℓ exp ( z ) = log ( 1 + exp ( − z ) ) \ell_{\text {exp}}(z)=\log(1+\exp(-z)) ℓ exp ( z ) = log ( 1 + exp ( − z ) )
目标函数: f ( w , b ) = λ 2 ∥ w ∥ 2 + log ( 1 + exp ( − y i ( w T x i + b ) ) ) f(w, b)=\frac{\lambda}{2}\|w\|^{2}+\log(1+\exp(-y_{i}\left(w^{T} x_{i}+b\right))) f ( w , b ) = 2 λ ∥ w ∥ 2 + log ( 1 + exp ( − y i ( w T x i + b ) ) )
对 w 求偏导: ∂ f ∂ w = λ w − y i x i exp ( − y i ( w T x i + b ) ) 1 + exp ( − y i ( w T x i + b ) ) \frac{\partial f}{\partial w} = \lambda w- \frac{y_i x_i \exp(-y_{i}\left(w^{T} x_{i}+b\right))}{1+\exp(-y_{i}\left(w^{T} x_{i}+b\right))} ∂ w ∂ f = λ w − 1 + exp ( − y i ( w T x i + b ) ) y i x i exp ( − y i ( w T x i + b ) )
对 b 求偏导: ∂ f ∂ w = − y i exp ( − y i ( w T x i + b ) ) 1 + exp ( − y i ( w T x i + b ) ) \frac{\partial f}{\partial w} = - \frac{y_i \exp(-y_{i}\left(w^{T} x_{i}+b\right))}{1+\exp(-y_{i}\left(w^{T} x_{i}+b\right))} ∂ w ∂ f = − 1 + exp ( − y i ( w T x i + b ) ) y i exp ( − y i ( w T x i + b ) )
η t \eta_t η t 学习率需要随着训练的次数不断的进行调整。具体公式为:
η t = 1 λ t \eta_t = \frac{1}{\lambda t}
η t = λ t 1
其中 $ \lambda = \frac{1}{nC} $, t 是当前迭代的次数。
1 2 3 4 5 for t in range (1 , T+1 ): eta_t = 1 /(lambda_*t) ...
根据 软间隔SVM理解 中的求导结果:
1 2 3 4 5 6 7 8 9 if loss_type == 'hinge' : st = y_i * (np.dot(W.T, x_i) + b) if st < 1 : W = W - eta_t * (lambda_ * W - y_i * x_i) b = b + eta_t * y_i else : W = W - eta_t * (lambda_ * W)
1 2 3 4 5 6 7 8 elif loss_type == 'exp' : exponent = -y_i * (np.dot(W.T, x_i) + b)[0 ] if exponent < 3 : W = W - eta_t * (lambda_ * W - y_i * x_i * np.exp(exponent)) b = b + eta_t * y_i * np.exp(exponent)
1 2 3 4 5 6 7 8 elif loss_type == 'log' : exponent = -y_i * (np.dot(W.T, x_i) + b)[0 ] if exponent < 3 : W = W - eta_t * (lambda_ * W + (- y_i * x_i * np.exp(exponent)) /(1 + np.exp(exponent))) b = b + eta_t * (y_i * np.exp(exponent)) / (1 + np.exp(exponent))
注:
在指数损失和对率损失中存在指数操作,具有不稳定性,所以需要在计算指数之前对指数进行判断,当指数过大时,则跳过该样本。具体比较的值设置为3。i f − y i ( w T x i + b ) < 3 if -y_{i}\left(w^{T} x_{i}+b\right) < 3 i f − y i ( w T x i + b ) < 3
整体代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 def pegasos (train, test, C, T, loss_type='hinge' , func_interval=100 ): train_x = train['X' ] train_y = train['y' ] test_x = test['Xtest' ] test_y = test['ytest' ] num_train = train_x.shape[0 ] num_test = test_x.shape[0 ] num_features = train_x.shape[1 ] lambda_ = 1 / (num_train * C) W = np.random.randn(num_features, 1 ) b = np.random.randn(1 ) func_list = [] choose = np.random.randint(0 , num_train, T) for t in range (1 , T+1 ): eta_t = 1 /(lambda_*t) i = choose[t-1 ] x_i = train_x[[i]].T y_i = train_y[i] if loss_type == 'hinge' : elif loss_type == 'exp' : elif loss_type == 'log' : t += 1 if t % func_interval == 0 : func_ = func(train_x, train_y, W, b, lambda_, loss_type) func_list.append(func_) print ('t = %d, func = %.4f' % (t, func_)) accuracy = 0 for i in range (test_x.shape[0 ]): res = np.dot(W.T, test_x[i].T) + b if res >= 0 and test_y[i] == 1 : accuracy += 1 elif res < 0 and test_y[i] == -1 : accuracy += 1 accuracy = 100 * accuracy / num_test print ('accuracy = %.1f%%' % accuracy) return accuracy, func_list
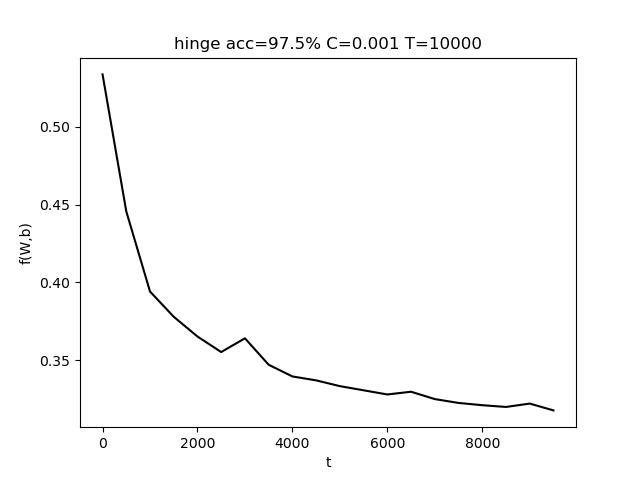
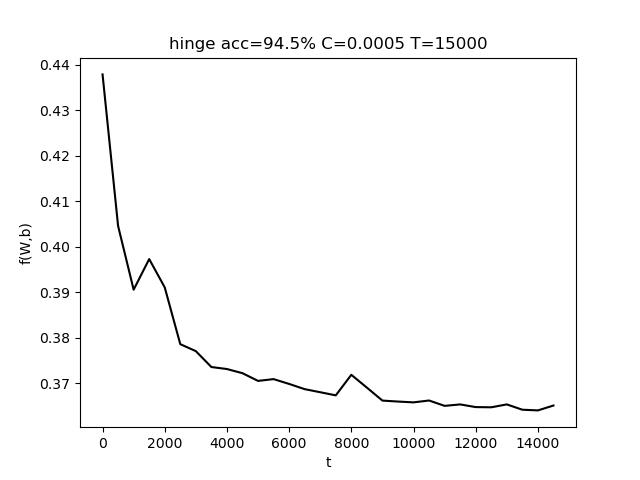
每次测试8次,取结果最好的那次。尝试使用了3种loss:hinge、指数损失和对率损失。三种loss的结果均达到了 90% 以上。
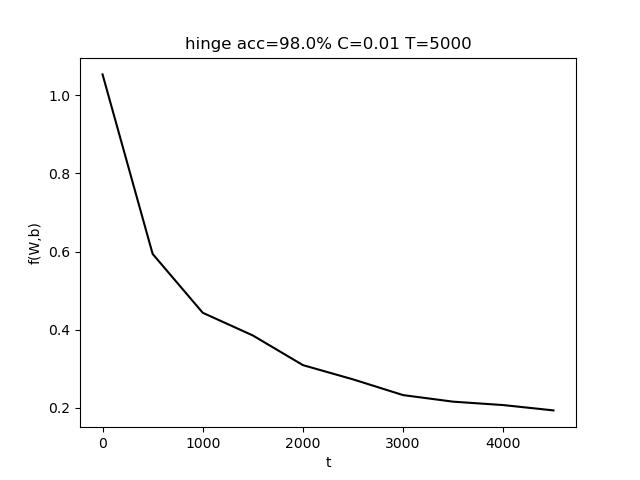
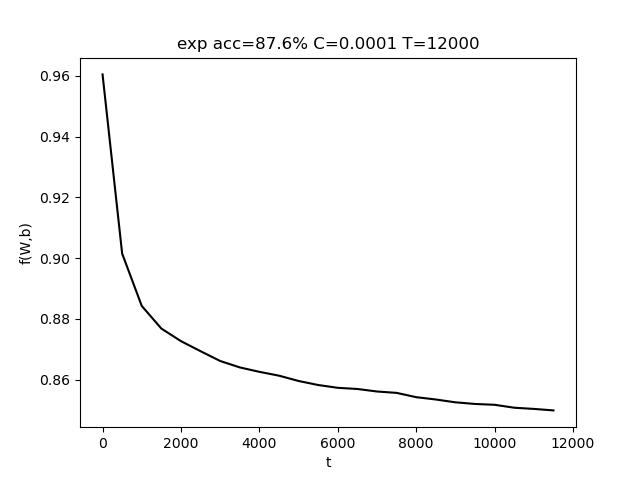
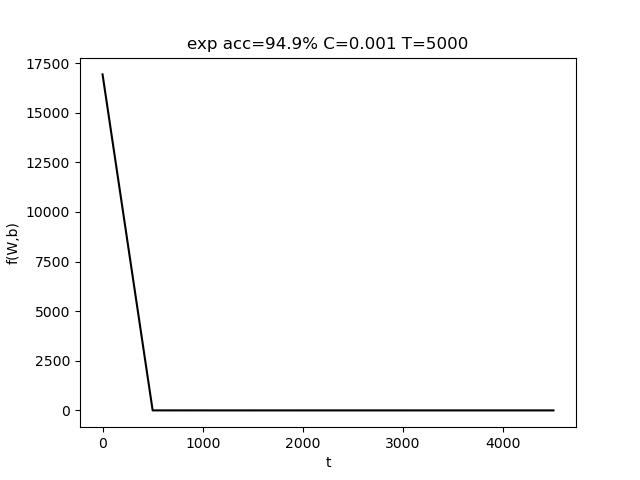
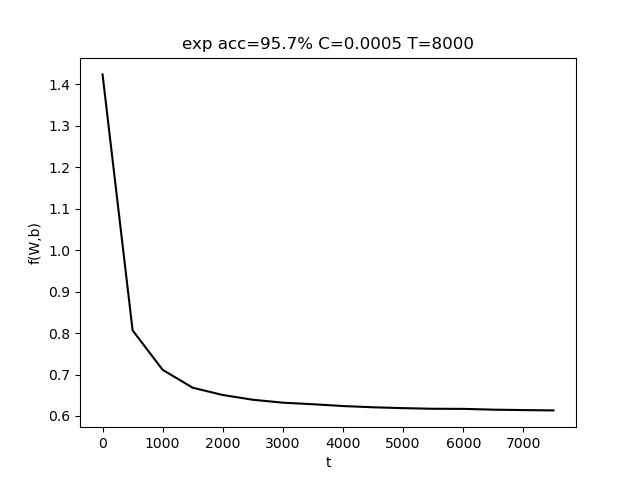
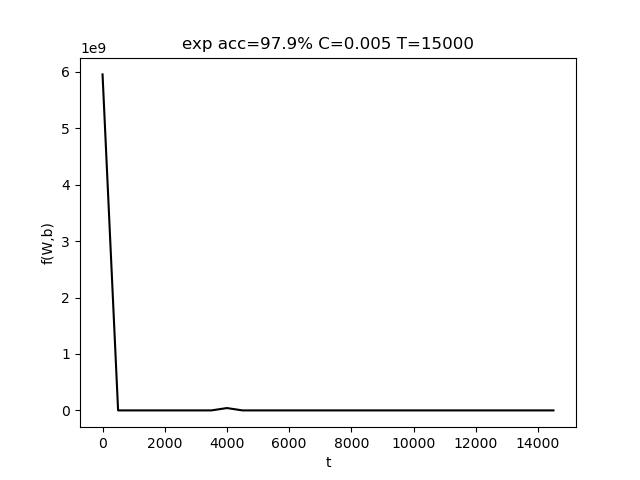
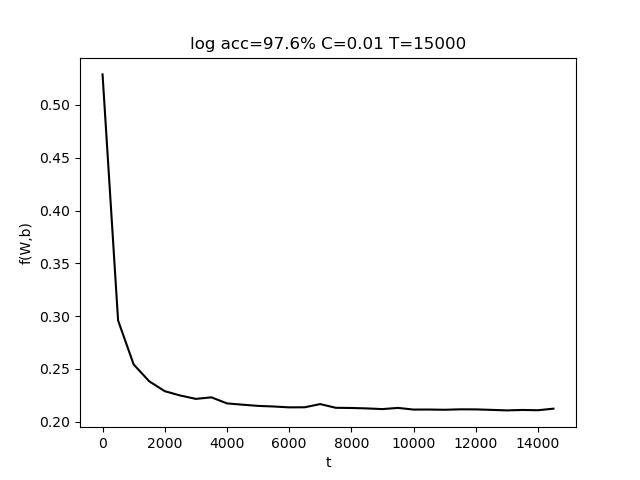
使用的参数为 C=0.001, T = 10000,最终准确率 acc = 97.5%
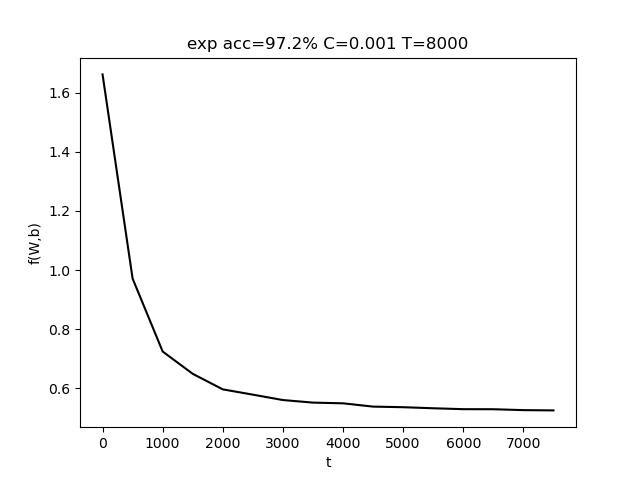
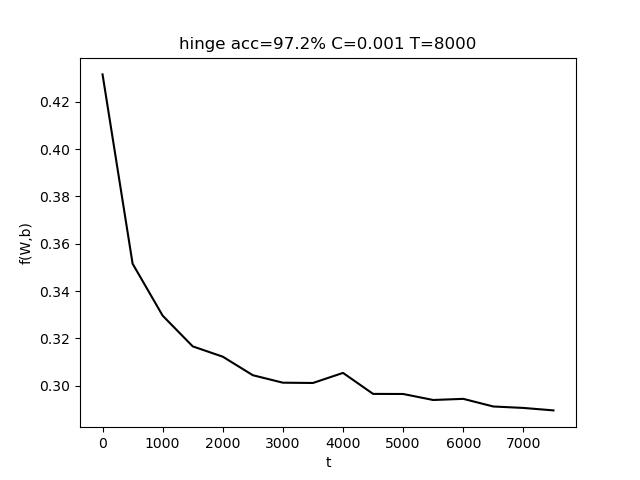
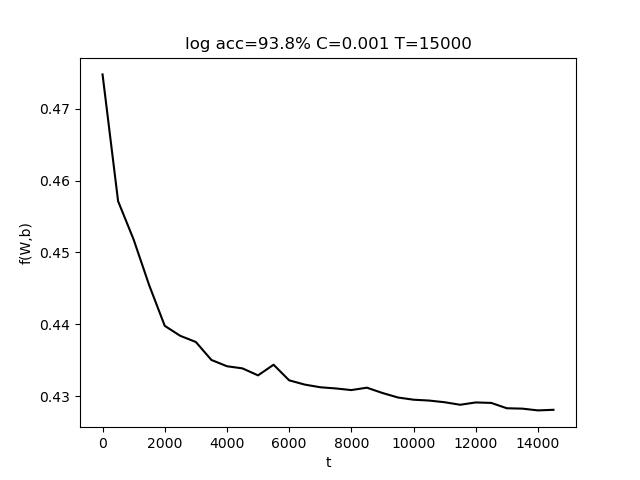
使用的参数为 C=0.001, T = 8000,最终准确率 acc = 97.2%
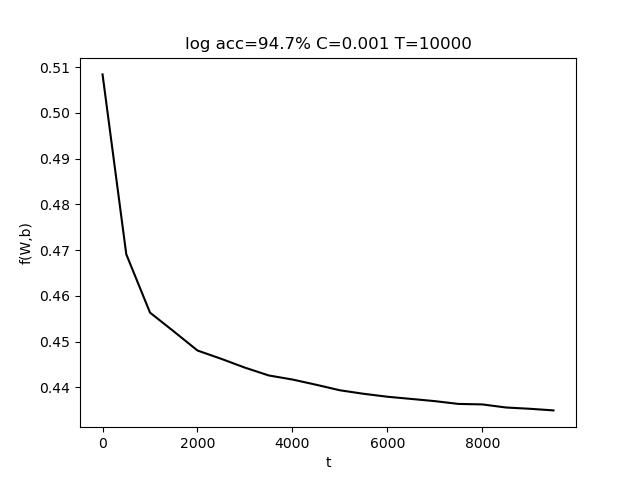
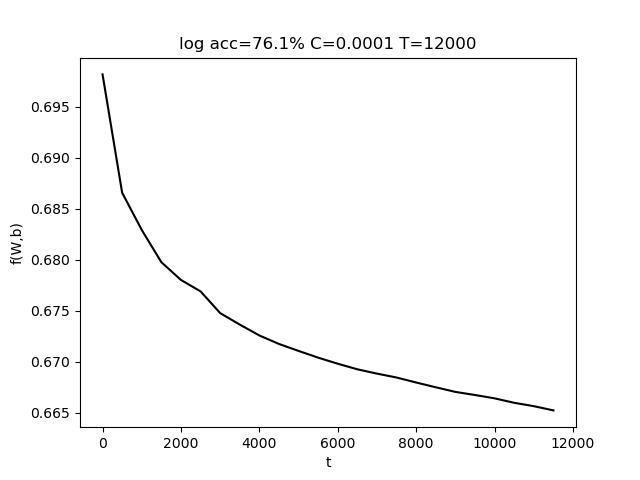
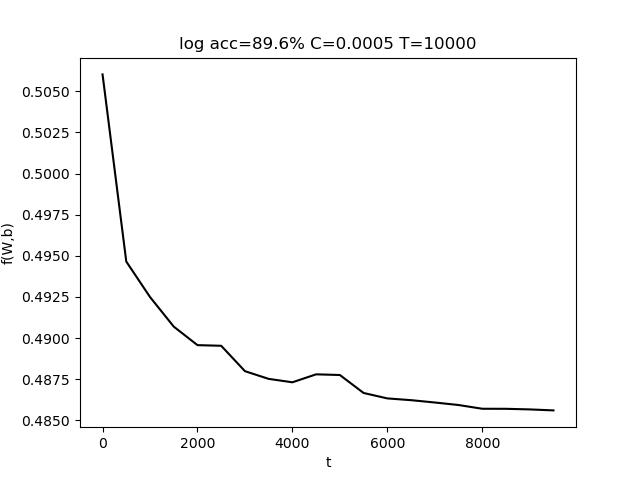
使用的参数为 C=0.001, T = 10000,最终准确率 acc = 94.7%
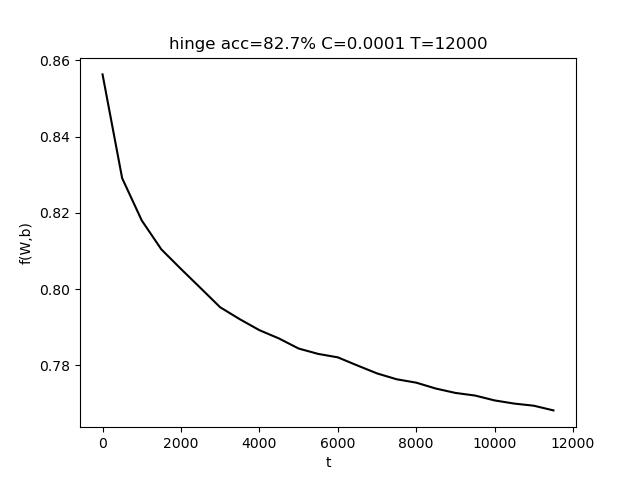
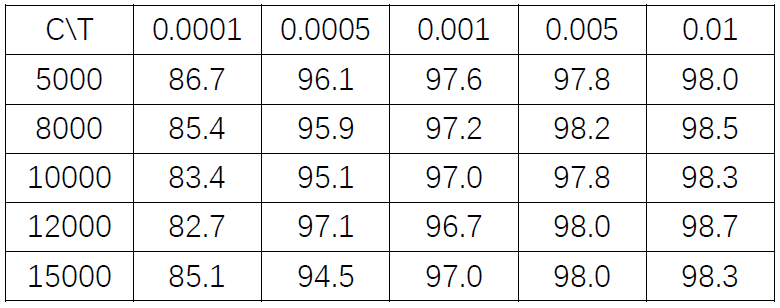
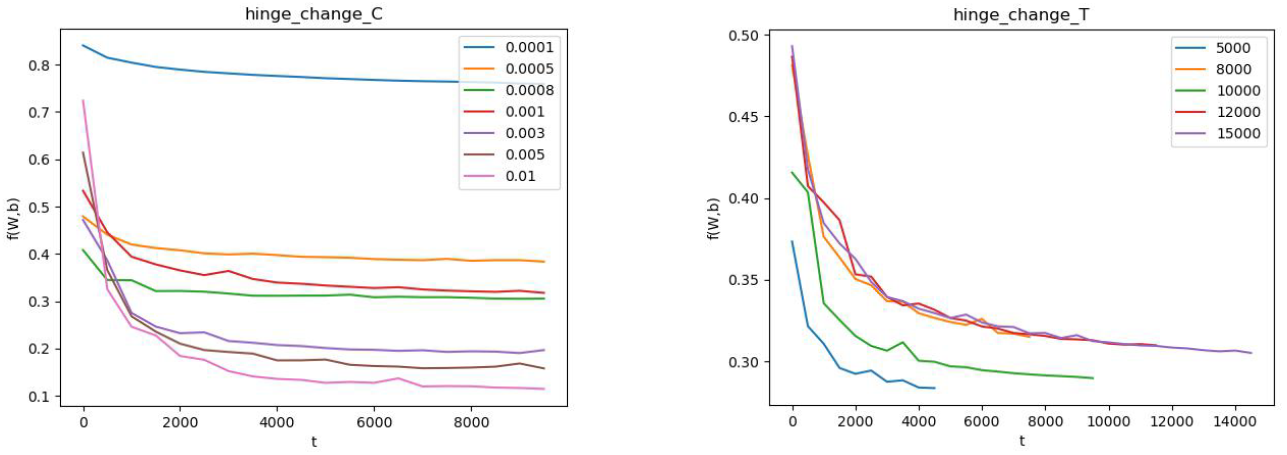
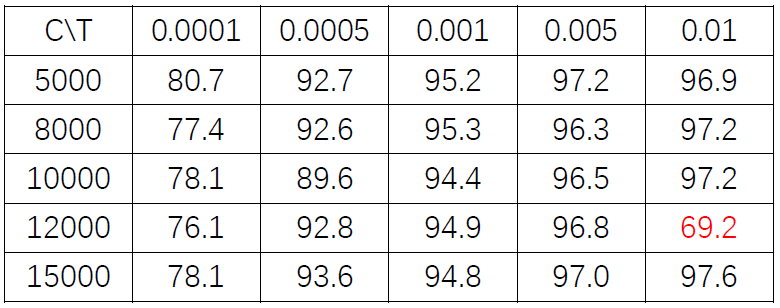
表格中,行代表C的变化,列代表T的变化。T的变化对结果带来的影响比较小。而适当增大C有助于提高准确度。
C 是惩罚参数,C值大的时候对误分类的惩罚增大,C值小的时候对误分类的惩罚减小。
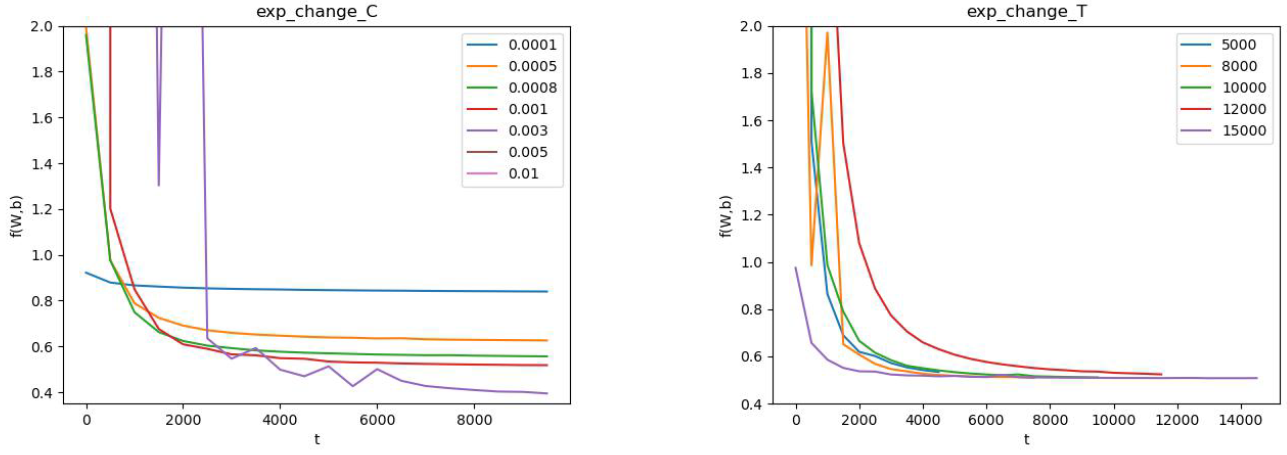
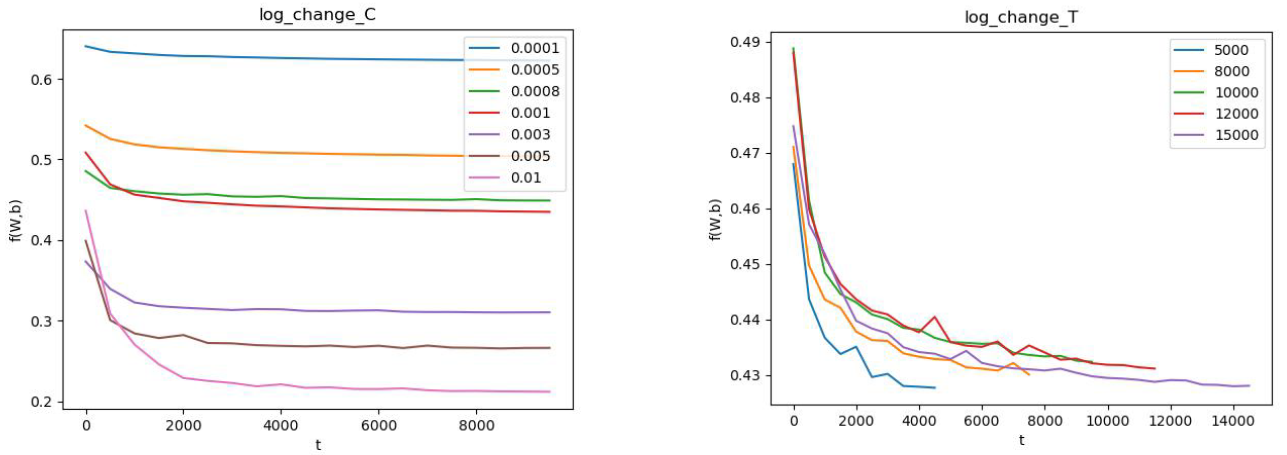
上图中,左图是固定T,改变C;右图是固定C,改变T。(由于使用随抽取样本,该结果存在一定的随机性)
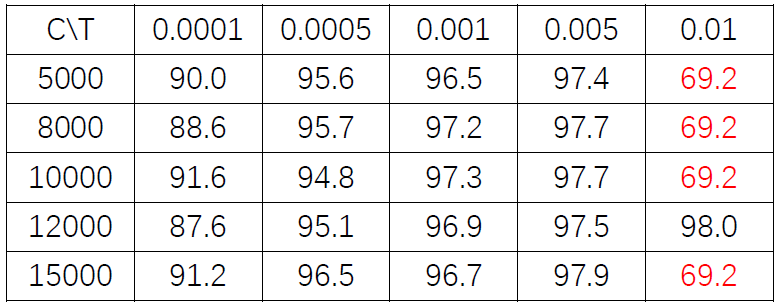
表格中,行代表C的变化,列代表T的变化。T的变化对结果带来的影响比较小。而适当增大C有助于提高准确度。红色数据表明,模型将样本全部判定为负,训练失败。
上图中,左图是固定T,改变C;右图是固定C,改变T。(由于使用随抽取样本,该结果存在一定的随机性)
表格中,行代表C的变化,列代表T的变化。T的变化对结果带来的影响比较小。而适当增大C有助于提高准确度。红色数据表明,模型将样本全部判定为负,训练失败。
上图中,左图是固定T,改变C;右图是固定C,改变T。(由于使用随抽取样本,该结果存在一定的随机性)